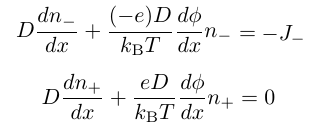|
<電流が流れることの意味>
|
<できるだけ簡単なモデルで考える>
電流が流れない前のページではA+, B-が溶けている系を考えましたが、
ここではB-が+極で電子を渡した後の生成物Cを考えます。
この逆反応によって B- が生成しますが反応速度が十分遅いものとします。 従ってφはA+とB- の空間分布で決まります。 |
|
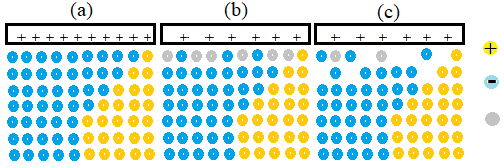
<電圧を上げると何が起きるか>
(a) 電流がはまだ流れないEDL(前ページの状況)。
|
|
|
<数式で表すと>
図では+イオンは動かず、−イオンが動いて電流になっています。この状況をフラックス(流束)で表します。
|
<基本方程式>
こうして得られた方程式を、x はデバイ距離でφはVTでそれぞれスケーリングして次の式を得ます。
|
|
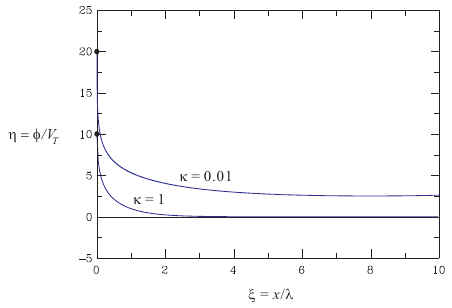
<電流が流れているときの EDL(η0=20)>
|
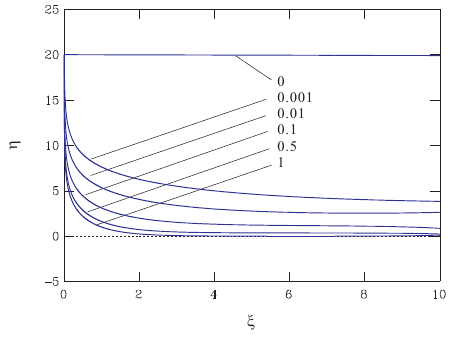
<電圧を上げていくと>
η0=10 では電流が流れないがη0=20 では定常的に電流が流れる場合、下図のような半定性的な図が描けます。
|
| <計算結果が意味すること>
電流が流れないとき(ページ(3)、0.25 V)、電場はEDLで完全に遮蔽されます。電流が流れたのならばEDLは広がり、電場は外に出ますが、強さは | <電子移動の多様性>
ーイオンが抜ける過程のほかにも+イオンが増える過程、あるいは両者が同時に起きる過程がありえますが、
ここでの取り扱いより複雑になるでしょうか。
|