30個の実験データ x_i (i=1..N)を小さい順に並べ、x_iを横軸に、i を縦軸に取ってグラフ化します。 原著では乱数を使う次のコードで処理しています。

1. from scipy import *
2. x = 8.5 + randn(30)
3. xr = x.sort().round(2)
4. from plotsvg import *
5. autoplotc(xr,title='Cumulative distribution')

1. code 2.1bb.py･･･テキストp.8の乱数データをcsvファイル (その内容)から読み込む。右図はその結果です(ndata=30)。
2. code 2.1cc.py･･･乱数をその都度発生させてデータとする。 同一のデータについて縦軸が均一のグラフと重みつきのグラフを描きます。と 右下の二がその結果です(ndata=200)。

上右の図は隣接する(x_i,y_i) を __| のパターンでつないだものですが、グラフとしては 隣接する節点(u_k,v_k)間に直線を引いたものとなります。max k は max i の倍です。 この作業は一つのモジュールとしてまとめておくとプログラミングが楽になります(Modula-2 では当然の発想です)。 というわけで次のようなモジュールを試作しました。

• hwbfiles･･･テキストファイルを読んでデータを得る。
• hwblines･･･(x_i,y_i)を(u_k,v_k) に変換する。縦軸はデータ数またはパーセント。 y_iの初期値は1だが(右の図)、重みをつけることもできる(右下の図)。
• statpos･･･平均値等に対応するグラフ上の位置を出す。

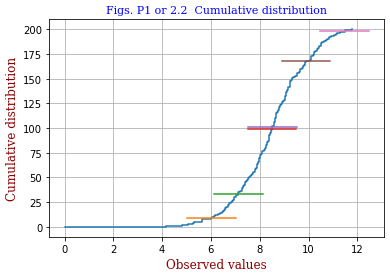
code 2.1cc.pyでは、 正規乱数 x_i(i=1,200) を200個発生させて小さい順に並べ、x_iを横軸に、i を縦軸に取ってグラフとしています。 データ毎の幅を一定として描いたグラフが真ん中の図です。 データ数が多くなるに従って誤差関数 erf(x) に近づくことが想像できます。

＜縦軸の目盛り間隔に傾斜をつける＞

目盛りの取り方を工夫すれば上の曲線的グラフを直線的なものに変えることができます。ここでは各データ幅を 　　w_i ∝ 1/gauss(x_i-av,σ) としています。gauss関数の 0.5/σ²とあるのを0.3/σ²として描いたのが右図です。 ±σ 等の位置を表す横線が中心に向かって移動していますが、中心付近でデータ密度が高いことを反映しています。