|
<問題の意味>
誕生日を手当たり次第に聞いていきます。 何人目で同じ誕生日の人に出くわすでしょうか? 例えば 1/5, 5/9, 9/12, 3/20, 9/12 と続けば r=5人目で出っくわしたことになります。 話を簡単にするために誕生日は n=365個あるものとします。 乱数を用いて誕生日を生成すれば r の度数分布、そして確率分布が得られます。 10000回試行して得られた確率は右のガタガタの線りです。滑らかな朱の曲線は右下の式で得られたものです。 <r の定義域> 出っくわす、あるいは集まるのは2回目以降、つまり r≧2です。一方、最悪の場合、n回やってもバラバラになります。その次は絶対にうまくいくので r≦n+1 となります。 | 
|
|
<r-1 人目まで誕生日が異なる確率>
1〜(r-1)人はすべて誕生日が異なります。その確率はnPr-1/nr-1です。 <r人目で誕生日が一致する条件付き確率> r-1 人目まで不首尾という条件のもとで同じ誕生日の人が現れる確率を求めましょう。 既に現れた1〜(r-1)人の誕生日と同じでよいから確率は (r-1)/n です。 <r人目まで誕生日が同じになる確率> 以上2つの確率の積をとって右の式が得られます。 | 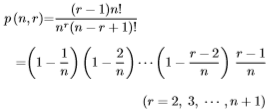
|
|
<ゲームにたとえる>
上からボールが転がってきてスロットに収まるゲームにたとえましょう(n=15)。
(a) は同じスロットに2つたまるまでボールを落とすゲームで、ここまで考えてきた過程と同じです。 | 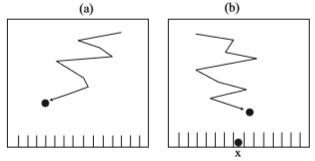
|