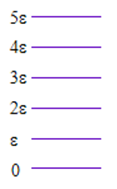
分子には激しく運動するものと穏やかに運動するものが混ざっています。 それを、かくかくのエネルギーをもった箱の中に分子が入っていると表現しましょう。 もっと簡潔には、分子はかくかくのエネルギーをもっているといいます。 ちなみに科学では「かくかくのエネルギー準位に分子が存在する」といいます。

問題はこうです。分子の個数と分子がもつエネルギーの総和を指定したら、分子はどのように箱に配分されるでしょうか?

＜分子が入る箱＞

話を簡単にするために箱に割り振られるエネルギーが右図の通り等間隔であるとします。 図では6箱しかありませんが、無限にあると考えて構いません。

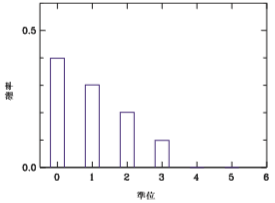
N=3個の整数乱数を発生させます。もし整数の和がM=3に等しければ成功となり、それぞれの出現頻度を一つ増やします。 例えば、乱数が 0,0,3 であれば 0の個数を2つ、3の個数を1つ増やします。 成功の回数が100になった時の結果が右の通りです。 上の箱ほど数が減っていますが、直線的に下がるのはNが小さいからです。

j番目の箱に入った個数をx_jとすると、分布は
(x₀, x₁, x₂, x₃,･･･)
で表せます。0,0,3（0が2つ、3が1つ）であれば (2, 0, 0, 1, 0, ･･･)です。

N=10個の整数乱数を発生させます。整数和がM=10に等しければ成功です。100回成功するまで試行した結果が右の通りです。 点線の指数関数によくあっています。

N, M が大きくなると、つまり実際の分子の世界では x_jの存在確率が指数関数 exp(-ε_j/kT) に比例することがわかっています（kはボルツマン定数、Tは絶対温度）。 この指数分布を特にボルツマン(Boltzmann)分布といいます。自然科学の基本原理です。

右は2つの成功事例です。左は (4,4,1,0,1,･･･)、右は(6,0,3,0,1,･･･) です。このようなパターンは何種類もあり、それぞれが繰り返して出てきます。 重みを考慮してパターンを平均（加重平均）したものが上の分布になるわけです。