(1) の続きです。右図のような分布パターンを加重平均すればボルツマン分布になるといいました。 そこで分布パターンの数え上げとそれぞれの重み（相対頻度）の計算をやってみましょう。 まず、 分子数がNであることを
x₀+x₁+x₂+x₃･･･=N
とします。エネルギーについては、箱に割り振られたエネルギーが等間隔であるとして
0･x₀+1･x₁+2･x₂+3･x₃･･･=M
とします（見やすくするために 0を掛けてあります）。

条件にあう(x₀, x₁, x₂, x₃,･･･) の重みを W とすると、Wは多項分布の式で得られます。

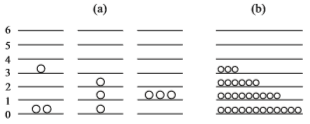
N=3, M=3の場合を調べましょう。上の2つの式を満足するパターンは右の(a)の通り3通りになります。 それぞれの重みは、左から順に W=(2+1)!/2!1!=3, (1+1+1)/1!1!1!=6, 3!/3!=1 です。

それぞれの箱に入った個数を数え上げると(b)になります。例えば 0 の箱には 2×3+1×6+0×1=12 の相対頻度で分子が入ります。 (1) のシミュレーションで求めた分布によく似ています。

現実の原子・分子の世界ではNもMも極めて大きな値になるので、場合分けや数え上げは無理です。 そこで、重みが一番大きい分布が支配的であると考えます。ただし、重みそのままではなく重みの対数を調べます。

右が対象とする関数で、αとβは未定乗数というパラメータです。x₀等で偏微分すれば指数関数分布が導かれます。

f = log (x₀+x₁+x₂+x₃･･･)!/x₀!x₁!x₂!x₃!･･･
+α(x₀+x₁+x₂+x₃･･･ - N)
+β(x₁+2x₂+3x₃･･･ - M)