|
<問題の意味>
「もらえない人が出るような配り方をするなんて人としてどうなんだ」と突っ込みが来そうですが、ランダムに配れば起きえます。 どうやって配るかというと、各々の林檎が配られる先をその都度ランダムに決めるのです。 <ランダムな配分エクセル流> 右図でF3〜F8は =INT(3*RAND())+1 で、6個の林檎の分配先を表します。 例えば3ならCさんの欄に●が表示されます。 ●を数えた9行目(1,3,2)が1回の試行になります。 |

|
|
<コンピュータシミュレーション>
(1,3,2)の次は(多分)別の配分パターンが現れます。とれをいちいち記録するのは疲れますからプログラムを書いて処理させます。 2000回試行した結果が右です。(0,0,6)は(6,0,0),(0,6,0),(0,0,6)を合算したものです。 もらえない人が出る確率は、0 が現れる確率の和ですから 0.6+4.2+12+7.6=24% といえます。 |

|
|
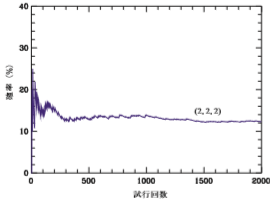
シミュレーションの泣き所は精度が低いことです。右は(2,2,2)の出現頻度を2000回まで調べたものですが、3桁まで読み取るのは難しい。
パターンの数に目を向けましょう。(a,b,c)の型が3, (a,a,b)の型が3, (a,a,a)の型が1でそれぞれ6通り、3通り、1通り。パターンの数は 3×6+3×3+1×1=28 です。この値は xA+xB+xC=6 の非負整数解の数 3H6 に等しいことが判ります。 |
|