もられない人が出てもいいから「とにかく」配る方法の数は、(2)の式でA, B, C を取り去って3⁶通り。

＜1人を避け、残りの2人にとにかく配る＞

Aに配らないことにします。B,Cの2人に「とにかく」6個の林檎を配る方法は2⁶通り。 配らない人をBとCにかえて結局 ₃C₁×2⁶通り。 ただし、配られない人が2人以上になる場合も含まれるので注意が必要です。

配らない人を2人にし、残りに「とにかく」6個の林檎を配る方法は

₃C₂×1⁶通り。 配られない人がこれよりも多くなることはありません。

＜答え＞

もらえない人が少なくとも1人になる確率は

P=(₃C₁×2⁶-₃C₂×1⁶)/3⁶=7/27=25.93%

r個のモノをn個の箱に分けるが、空の箱は1つ以上できる。その確率を求めます。3→n, 6→r とおいて

P=[_nC₁×(n-1)^r-_nC₂×(n-2)^r+･･･]/n^r
=_nC₁(1-1/n)^r-_nC₂(1-2/n)^r+_nC₃(1-3/n)^r-･･･±1/n^r-1

で計算できます。

右の図が確率のグラフです。横軸は各箱に配られた平均値で、これが同じでも箱が多いほど空っぽの箱ができる可能性が高くなります。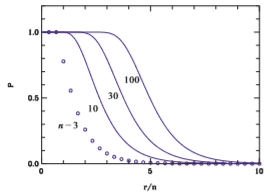