|
<燃料電池の出力損失 (1) Reaction rate loss>
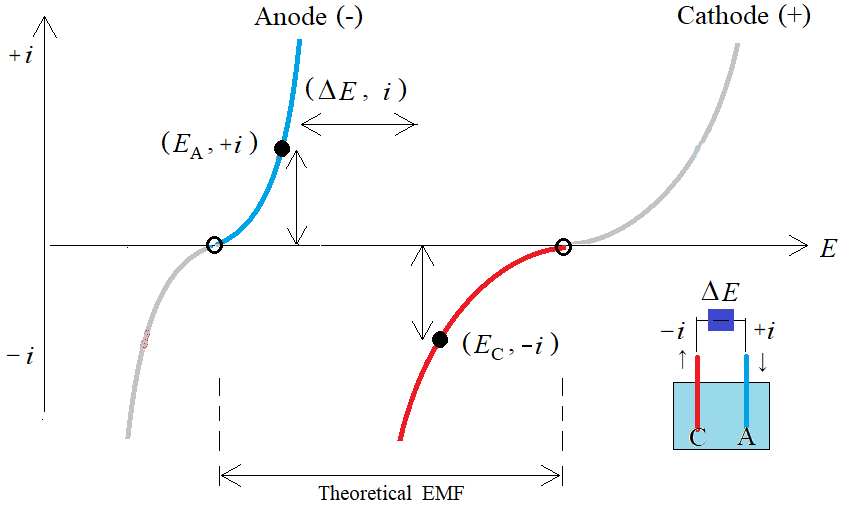
一般に電池の出力電圧は、出力電流が増えるに従って低下します。このようすをモデル計算で理解しようというのがこのページの目的です。 まず取り上げるのは、電圧をかけなければ電流が流れない、逆に電流が流れれば必ず電極に電圧がかかっているという電池の本質に根ざした損失です。 これを図示記したのが右の図で、二つの Butler-Volmer関数 i=f(E) が描かれています。 二つの ○ の間隔は起電力 EMF に相当します。次に正極 (カソード) から i の大きさの電流が流れるようにすれば、符号は負なので(電極に流れ込めば符号を正とします) 赤い分岐の●が動作点です。同じ大きさの電流が負極 (アノード) に流れ込みますが動作点は青い分岐の●です。両方の●の間隔が出力電圧になります(図のΔE)。 i が大きくなれば●は軸から遠ざかるので出力電圧は小さくなります。 |
<電流密度 i と電圧 E の間の関係>
|
|
<燃料電池の出力損失 (2)> 上では、電流が同じになるような電圧の位置を i=f(E) のグラフ上で探しましたが、f-1(i) から直接に E を求める方が簡単です。つまり 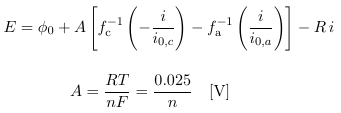
i-E の関係式の両辺を A で割ると無次元変数の間の式に変換できます。以後、これを計算します。 
|
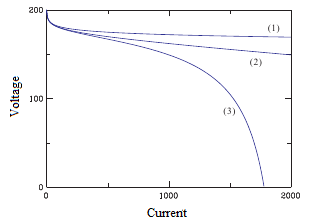
<燃料電池の出力損失 (3) Reaction rate loss + resistance loss> y0=200 として計算したのが下の図です。 抵抗がなければ破線(a)のように対数関数的に電圧が下がります。現実にはこのような振る舞いは見られません。 (b) はr=0.05 の抵抗がある場合のグラフです。直線的に電圧が低下しています。 この図を見ると 電圧がゼロになるまで(b) の直線を延ばすことができそうに思えますが、実際にはある電流値を超えると燃料の供給も生成物の排出も間に合わなくなって出力電流が低下します。 
|
|
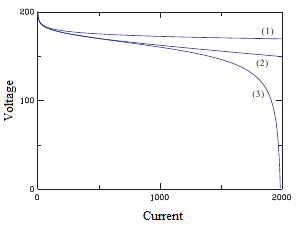
<燃料電池の出力損失 (4) +Transport loss> 出力低下のようすは次式でアタリをつけることができます。 
|
<燃料電池の出力損失 (4) Transport loss の別の形> 上の計算式は拡散が主因の場合はよいのですが、常にそうとは限りません。そこで次の経験式に拡張してみます。 
|