π=3.14･･･を最初から r 桁ずつ読んでいきます。数字がすべて異なる数字なら success（成功）、 そうでなければ failure（失敗）です。r=5 について3回試行すると右の通りです。 ちなみに条件にあうもの・あわないもの2通りの結果を生じる試行のことをベルヌーイ試行といいます。 さて、成功の確率はいくつになるでしょうか?

31415･･･failure
92653･･･success
58979･･･failure

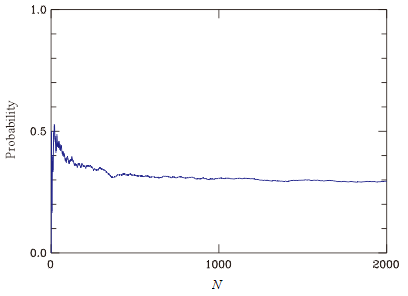
私のとった方法です。インターネット上に"100,000 Digits of Pi.htm"というファイルがあったのでディスクにダウンロードしました。 作者はM.D. Huberty, Ko Hayashi & C. Vang の3氏です。

そのファイルをプログラム（Pi10000）で開いて3.14が書き込んである場所を探します。 そこから数字を5桁ずつ読んでいきます。その回数がNです。 その際、数字がすべて異なっていればMとして回数をカウントします。そしてN対M/Nのグラフを作ります。

右は2000回の試行結果です。確率は 0.30 であるといっていいでしょう。

パイは無理数ですから数字はランダムに現れると考えられます。 従って、「0〜9を要素とする箱（母集団）から 5個の要素をランダムに取り出すとすれば、要素がすべて異なる確率はいくつか？」という問題に言い換えることができます。 より正確にいうと、取り出すという行為で要素の分布が変わることはない。これは自然科学では当然ですが、ゲームでは成り立たないことがあります。

「場合の数」の発想、つまり何通りになるかを調べて解くと右の通りになります。

最初に選べる数は10通り。2つ目に選べるのは、最初の数を除いた9通り。3つ目に選べるのは8通り。こうして、すべての数字が異なる 5桁の数の個数はb=10×9×8×7×6=₁₀P₅=30240。

よって確率は b/a=0.3024

この問題はいろいろと改変できます（右）。

1. 桁数はr=5に限定する必要はない。

2. 「全部異なる」以外にも数字の出方はありうる。例えば全部同じとか。