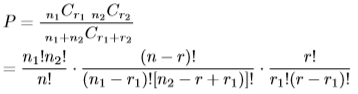数字を挙げて説明します。有権者数10,000人の町で町長選挙があります。 現町長と新人が出馬することになりました。 実は全員がどちらを支持するか既に決めていて、現職支持が5,500人、新人支持が4,500人です。 ですが、このことは神様しかご存じありません。

さて、ある広告会社が町民100人をランダムに選んでアンケート調査をします。 新人が勝つという予想が出る確率は?

浮動票を考えないのが非現実的ですし、「確率」という言葉に違和感も感じますが、 ランダムサンプリングを具体的に考えると少し分かった気になります。

まず有権者に対して適当に1〜10,000の番号を割り振ります。そしてその中から100個の数字をランダムに 取り出すことがアンケート調査をすることで、そのたびに支持票の分布が出ます。 もしこの作業を何回も実施すれば、新人のほうに票が多く集まるというケースも出てきます。 それが「新人が勝つという予想が出る確率」です。

実際には一度しかアンケートはできないので、「もし何回もやったら」を頭の中で想像するわけです。 確率の意味が分かりにくいのはそれが理由でしょう。

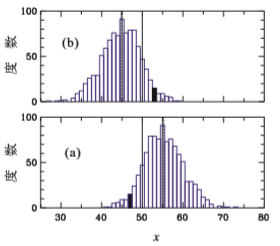
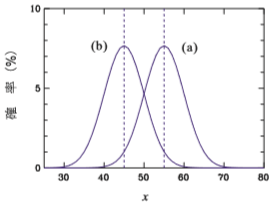
乱数 RAND() を使えば「100個の数字をランダムに取り出」せます。エクセルの流儀なら INT(10000*RAND()+1) を100回実行すればよいのです。そうすれば例えば 56票対44票という結果が出ます。

しかしこれでは確率にならないので、1000回繰り返しましょう。そうすれば右のような分布が得られます。 (a)は現職の得票数、(b)は新人の得票数です。一番可能性が高いのは(a)が55票付近、(b)が45票付近なので直感と合います。

しかし黒く塗ったところは(b)が53票で(a)が47票で新人の勝ち。つまり(b)であれば x>50 の部分が新人勝利の事象です。 その確率は約10%です。これを「10回アンケートをやれば1回間違った予想をする」と言ったりします。

組み合わせ問題として解いてみましょう。現職支持がn₁人、新人支持がn₂人、合わせて n人とおきます。ランダムサンプリンではそれぞれr₁票、新人支持がr₂票、合わせて r票とおきます。そのような状況が生まれる確率Pは次式で得られます。

r₁またはr₂についてグラフを描くと右の通りになります。上のグラフを滑らかにした形で、いわゆる正規分布になっています。 x=50%から先の裾野の面積が新人勝利の確率となります。