|
<問題の意味 (i)>
前回(2)ではランダムウォークの経路に制限をつけませんでしたが、今回は一度も原点に戻らないという条件をつけます。
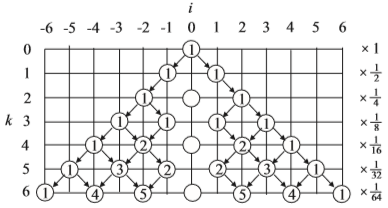
<経路ダイアグラム>
| 
|
|
<相対度数>
図のpa(i,k)を前回のpa(i,k)で割った比が右の図です。 pa(i,k)=(|i|/k)p(i,k) という関係のあることが分かります。 |
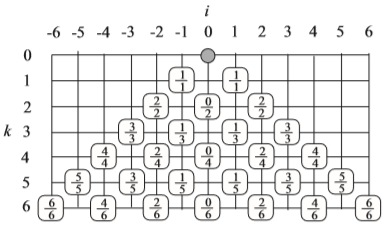
|
|
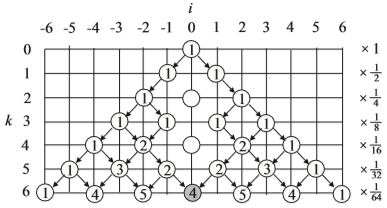
<問題の意味 (ii)>
原点には一度も戻らないが、最後に原点に戻る経路の確率を求めます。最後が k=6 であれば右図の通り 4/64 です。 <最後に原点に戻る確率 pb(k)> k歩目が最後だとすると、(k-1)歩までは一度も原点に戻らないので
pb(k)=[pa(-1,k-1)+pa(1,k-1)]/2=(1/k-1)p(1,k-1)
| 
|