ランダム（無作為）な試行のうちで最も簡単のは 「コインを親指ではじいて表と裏のどちらかを出す」ことでしょう。これをコイントスといいますが、 具体的にどうやるか知りたければ coin tossで検索してみてください。膨大な量の画像が出てきます。

さてあなたは、表が出たら〇、裏が出たら×と記録する係になっています。 しかしその記録紙を紛失してしまいました。再度繰り返すだけの時間はありません。 そこであなたは自分で書いてしまうことにしました。けしからん話ですが、ただの遊びです(笑)。 面倒くさければ右のマスを使いましょう。マークすれば〇、しなければ×とします。マスは100個ありますがこの倍はほしいです。

無作為というからにはテキトーに書いていけばいいはずです。実はこれが意外と難しいのです。 次のような独り言が聞こえてきそうです。 「最初は〇×〇×とする、少したったら〇〇と××を入れる、テキトーに〇〇〇と×××を散りばめる･･･。」 うまく行きそうですが、 そのうち「同じことを繰り返しているのでは?」「バランスが悪いのでは?」など、不安感に襲われます。 あるいは「どうせ分かりっこない」と居直ってしまうかもしれませんね。 この遊びが性格診断に使えるのではないかと思うのですが、はてさて･･･。

コインそのものは力学でいう剛体回転子なので、同じ強さで同じ場所をはじけば同じ運動をするはずです。 しかし表面と裏面で凸凹が違うので最初の面が表か裏かで着地の仕方がわずかに違うという実験があります。 実際には、はじき方やキャッチの仕方がその都度違うので ランダムであると信ずるわけです。詳しい話はネットにあります( Faletto2017, AAAS2004)。

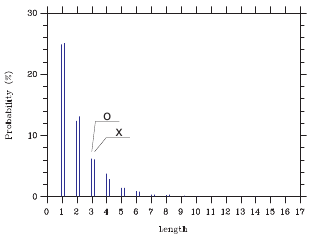
捏造に成功したかどうかを判定するには連続した並びの種類と個数を〇と×について調べましょう。これをH_k,T_kとします。 H₁は 単独の〇（パターンは･･･×〇×･･）の個数です。T₂は×が2つ並んだ組（パターンは･･･〇××〇･･）の個数です。 コイントスの総数は Σk H_k+Σk T_kに等しくなります。 200回程度ならk=1〜3個の連なりとk≥ の連なりの4種類を数えればいいでしょう。

＜シミュレーション結果＞

コイントスを10000回やったら右の結果が得られました(縦軸はパーセント)。kが大きいところは0回か1回しか現れません。しかもばらついています。 あなたの結果が図のデータに近ければ捏造は成功となります。