かつてBuffon氏が行なった有名な実験です。 まず罫線が間隔2aで引いてある紙と長さが2aの針を用意します。右図で長い線が罫線です(短い線は説明用の参考線)。 実験は簡単で、上から針を落とすだけです。ただし、針は跳ねないといけないので、ある程度の高さが必要です。 小さな紙では針が外に飛び出てしまいますから、B4かA3サイズがいいでしょう。 落とした針は、罫線の間に来ることもあれば、罫線にひっかかることもあります。が、 N回繰り返せば、ひっかかった回数Mの割合はある値Pに近づくはずです。 この値M/Nを求めようというのが実験の目的です。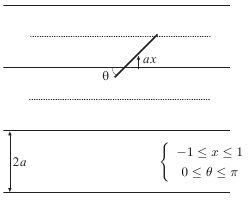

実際の実験をやる前に、針が転がったようすをコンピュータ上で再現してみましょう。 まず針の位置を記述することから。針の中心(重心)とそこに最も近い罫線との距離axで指定します(-1≤x≤1)。 次に針の端点は中心から±a sinθずれたところにありますから x±a sinθの符号が変われば罫線を挟んで位置することになります。 二つの一様乱数xとθをN回発生させたうちでこの条件が成り立つ回数Mを数えてグラフにしたのが右図です。 Nが大きくなるに従って比の値が約65%に近づくことが分かります。なお、Nが小さいところの振る舞いには随分とバラツキがあって次の2000個では 様相が全く違います。ですから100〜200回程度の試行では65%から大きくずれても驚くにはあたりません。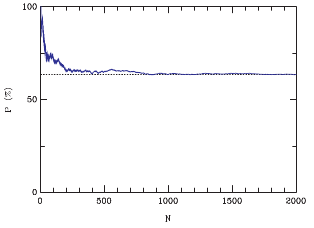

一様乱数x,θの組は長方形(右図の外枠)の領域中の一つの点になります。これらの点は、順番はランダムでも均一に平面を埋めていく、 つまり濃淡のムラは気にならなくなる、と考えられます。 一方、「x±a sinθの符号が変わる点」は右図の影の領域の中に均一に分布します。二つの領域の面積比が確率Pですから、計算するとP=2/π=63.7%が得られます。

＜実験をするにあたって＞

縫い針は怪我のもとですから爪楊枝あるいは長さをそろえた針金がよいでしょう。 M,Nのデータは人海戦術で得ることができます。実験に参加する人に罫線紙と針を配布すればよいのです。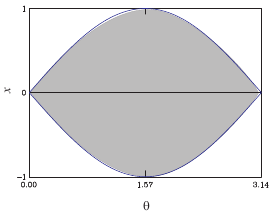