|
<2次元ランダムウォークを追いかける> 右図で〇が兎、●が狐と思ってください。どちらも一回に付き1歩ずつ上下左右に進みますが、動き方は全く違います。 〇はサイコロの目に応じて2次元ランダムウォークをします(6択のシミュレーション)。 ●はひたすら〇を追いかけますが、ランダムではなく考えながら追いかけます。そして 10歩を上限として●が〇に追いつければ●の勝ちです。〇が影の領域に逃げ込むか、●が〇に追いつけなければ ●の負けです。これはもはや確率というよりはゲームです(笑)。 当然のことながら〇が縁に近いか、〇と●が離れていたら●は負けやすくなります。 勝てる確率が50%程度ならゲームとして意味があるかもしれません。 | 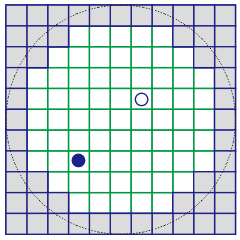 |
|
<●を動かすアルゴリズム>
シミュレーションによって駒の初期配置の適不適を知らべてみます。 そのために●を動かすアルゴリズムを右のようにしてみます。特にどの言語で書いたってことはないですが、意味は自明でしょう。 ちなみに、DxとDyはそれぞれ兎と狐の横方向および縦方向の距離です。 | 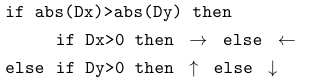 |
|
<シミュレーション例> 何回か試行したようすを右に示します。これを2000回繰り返すと狐が勝つ確率は54%でした。 この初期配置のもとでパソコンに代わって人間がプレーすれば結構楽しめるのでは? |