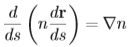| 太陽光は宇宙空間を直進しますが、地球の大気圏に入ると屈折率が1より大きくなるので屈折します。 そのため水平線の上に出る時刻がわずかに早くなります。この屈折角を見積もってみます。 |  |
| 光の経路を軌跡として記述するのがいわゆる幾何光学で、鏡による反射やレンズによる屈折が説明できます。
ところが物理学や電波工学では光や電磁波は波動であると習います。二つの見方には大きな隔たりがありますが、
間をつなぐ理論としてアイコナール(eikonal)理論があります。Max Born とEmil Wolf によるロングセラーの Principles of Optics
に詳しく解説してあります(第6版ならp.88)。一言でいえば電磁波の位相をアイコナールS(r)で記述します。そうすればSが一定の面が波面を形成するので
それをたどれば光の軌跡が得られるわけです。
実用上は、アイコナールを含まない式でもって軌跡を記述すると便利です。nが屈折率、sが光線に沿って進んだ距離です。 | 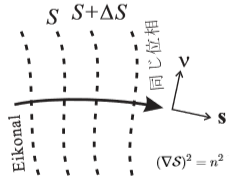
|
| この方程式を解くうえで有用なのが微分幾何学の方法論です。 それによれば曲率半径ρと接線ベクトルsそして法線ベクトルνでもって変形できます。 | 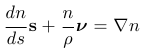 |
| 光線が(x,y)平面内に収まっているとします。そうすると非線形常微分方程式が得られます。 この式は屈折率そのものではなくてその対数の勾配で光線が決まることを示しています。 |  |
| いよいよ大気圏内の光線の話に入りましょう。座標を図のようにとります。
Pは光線の出発位置で鉛直線からθだけ傾いた場所です。ここから水平線方向に光線が出ます。
光線の途中の点P'は中心からρの距離にあります。屈折率がρのみに依存するのがこの問題のポイントです。
一方、気体の屈折率は n=1+αという形を取ります。αは原子や分子の電子分極に由来する因子で、原子や分子の数密度で決まります。 数密度の距離依存性をf関数で表しましょう。典型的なfは指数関数で、wが減衰の度合いを表します。 | 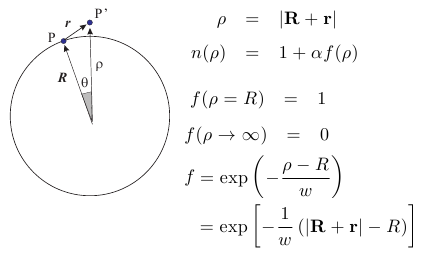 |
| 数値計算はR=6371、w=80、α=0.0003として計算した結果が図です。
ルンゲクッタ(Runge-Kutta)法で大気圏の倍程度まで8i92ポイント計算し、そのあとは5倍の粗さで同数解きました。
その時気づいたのですが、対数微分はどこまでも尾を引きます。大気圏の外側は真空なので対数微分はゼロとすべきです。
結局振れの角は-0.9°と求まりました。モデルが荒っぽいので数値そのものに意味はありませんが、 太陽光の屈折によって日の出が数分早まることはおおいにあり得る話だと思います。 (注)ここで用いたプログラムはEikonalRays 1.1で、nがyのみに依存する蜃気楼問題も解いています) | 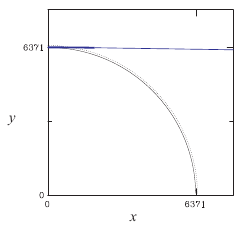 |