| Updating Python Code 0.1 (p.169) for Fig. 2.1 (p.7) and Code 2.1 (p.171) for Fig. 2.2 (p.7) |
|
<Original code 2.1.py>
30 data points xi (i=1..N) are arranged in increasing order and x is plotted against i.
The author made a simulation using random numbers.
- from scipy import *
- x = 8.5 + randn(30)
- xr = x.sort().round(2)
- from plotsvg import *
- autoplotc(xr,title='Cumulative distribution')
As anticipated, python did not recognize plotsvg, and I made two versions.
- code 2.1bb.py: Berendsen's data are written to a csv file (contents) and then fed to the program. The result is shown in the right.
- code 2.1cc.py: A set of random data is arranged, The x-axis is drawn in two ways. One is an ordinary axis with homogeneous spacings. The x-axis of the other is inhomogeneous such that spacings are narrower near 0% and 100% and wide at 50%, the details are explained elsewhere. The results are shown by two graphs in the right.
|
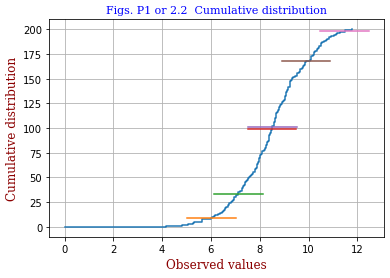
<Revised code2.1bb.py gives this graph>
|
|
<Making modules>
The tasks used for producing the graphs have been divided into the following modules. The modules are to be imported if necessary.
- hwbfiles...Read a textfile
- hwblines...Convert the original data (xi,yi) to plot data (uk,vk). Here vk is different from vm if m<>k. The spacing of the v-axis may be unity or may be inhomogeneous decreasing toward 0% and 100%.
- statpos...indicating the positions for the mean, median, mode, and standard deviation.
|
<Graphics output of code2.1cc.py>
|
|
<Plots of normal probability distribution>
Let the frequency yi be coverted to the probability Pi=(i-1/2)/n (i=1,..,n) and plotted against i. (Please check Wikipedia, Normal probability plot.)
The procedure may be made simple if the data are plotted on the so-called probability paper. If the data obey the normal distribution, the points tend to align in a straight line.
The procedure may be even simpler if the computer is used: The data are converted in accordance with the following equation.
where P is the accumulated probability and z the transformed x. For more detailed explanation please see (here). This equation has been derived so that (z,P)=(ε,ε), (1-ε,1-ε).
The code code2.2cc.py has given the result as shown right.
|
<Graphics output of code2.2cc.py>
|