|
(1) Outline
次の二階偏微分方程式と境界条件を考えます(Text p.132)。 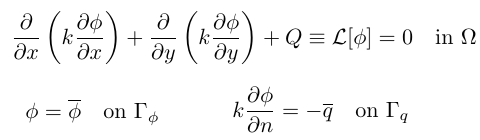
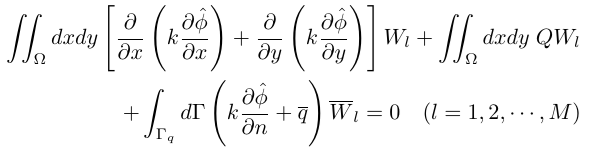
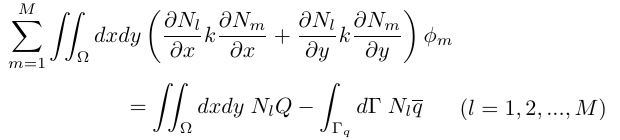
Ωを三角形または四角形の領域 Element(Ωe)に分割します。 
|
(2) Element and Node
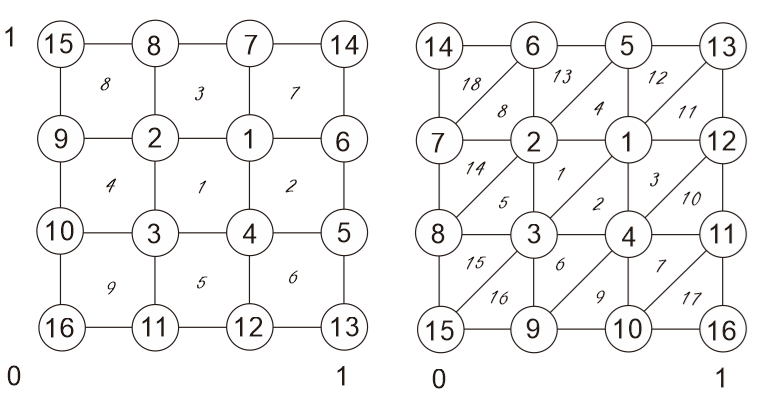
前項の Ω と Ωe の例を下に示します(Text p.146 を参考)。Element は左図で e=1〜9, 右図で e=1〜18 です。Node はどちらも1〜16です。 FEM では各Element について得られたKeφe=fe (Local equation)からKφ=f (Global equation)を組み立てます。Keの形はfeの形に依存します。
|
|
(3) Shape function
上では偏微分の形で現れましたが、Nie(x,y) をshape function といいます。e はElement, i はNodeです。Local model では三角形なら iは3個、四角形なら4個です。図上右では e=1 の (N1,N2,N3) とe=2 の
(N3,N4,N1)は同等です。
高次のshape function もあります。2次なら放物線も取り入れて組み立てます。 右図は三角形に対する2次の関数N6e(x,y) です (Text p.188)。 Mathematica で描きました。 |
(4) 2nd-order Shape function N5e(x,y)
Node は図の左端の頂点を 0 としてぐるりと左巻きに 1,2,3,4,5と進む。Node 1,3,5 は辺の中点。 N5eはNode 5で1を取る関数 (Text p.188)。 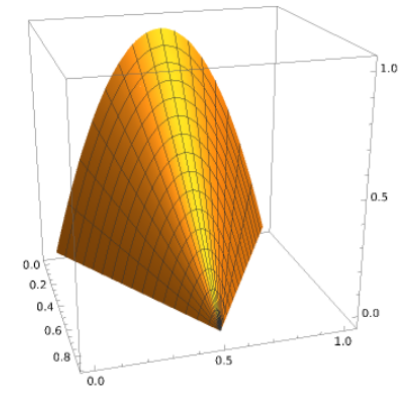
|
|
(5) keφe=fe and Kφ=f
上図の三角形 Element の場合、e=1 については 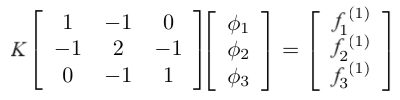
この関係式をすべてのElementについてAssemble すると φ1〜φ16についての連立一次方程式 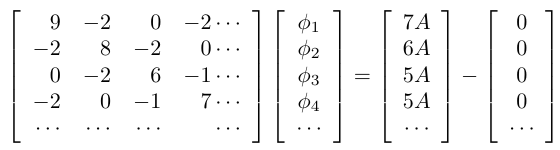
が得られます。右辺の第一項はQに由来する成分、第二項はNeumann型境界条件に由来する成分です。 |
(6) Dirichlet型境界条件
Node が n個あるものとします。Kφ=fはn元連立一次方程式です。 さて外界と接する m個の Node が任意の値に設定されているものとします。任意とはいっても現実を反映しています。 Kφ=fでいえば、m個の変数に値を代入したあとで (n-m)元の連立方程式を解くことになります。しかしそれは不可能です。 まず、係数行列式を調べるとn元では det(K)=0 ですが、1個目の境界値を代入すれば(n-1)元方程式の係数行列式は有限となり、方程式は解を持ちます。 しかしその解の中に次の境界値が含まれることは稀です。なおも境界値を代入していっても解は存在しません。 Text ではこれを問題視していないのでもしかすると私の理解が浅いのかもしれませんが、自分なりに策を練りました。
|