|
(1) Exercise 3.18
元々の Exercise 3.18 (Text p.148) は右図上のとおり Element が4, Node が6 です。手計算で解くことを想定したのかもしれません。物足りないので右下の図のように区画を増やした課題を作りました。赤い丸はLocal K-matrix の原点です。 境界条件は元の課題に準拠しました。Neumann型については公式
また、y=0 に沿った境界面では、φ=1-x2 という Dirichlet 条件を課する。 |
(2) Elements and Nodes
元の課題。 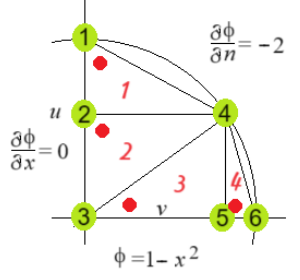
追加した課題。 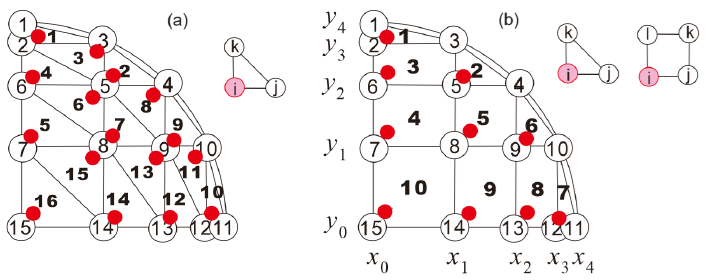
|
|
(3) Input text file
XDS Modula-2で作った FEM_practical2 ではテキストファイルからデータを入力します。例として Cylinder34.txt の内容を抜粋します。
% Exercise 3.18 extended 注釈
Elements=10 Elementの数
Nodes=15 Nodeの数
x1=0.404061018 座標情報
y0=0 座標情報
2=x0,y3 Node 2 の位置
#1,2,3,1|x1-x0,0,y4-y3 Element 1 の構成(三角形)
#3,6,5,3,2|x1-x0,y3-y2 Element 3 の構成(長方形)
~1,-2,{1,3},[x1-x0,y4-y3] Element 1 のNeumann条件
この内容を解読するために FEM_parse というモジュールを作りました。 |
(4) Result
(2) の「追加した課題」(b) を解いて下図が得られました。(x,y)平面は Node 配置を表わし、z 方向に延びる直線は各 Node のφ値を表わします。 (a) は InsertPhiToKr を、(b) は LSQnode をそれぞれ用いて解きました。 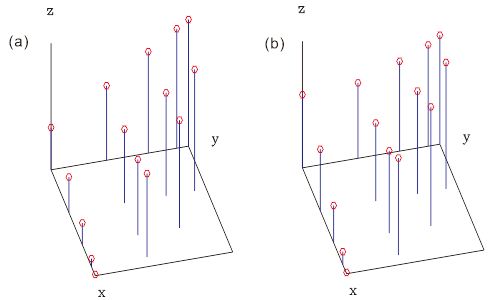
|