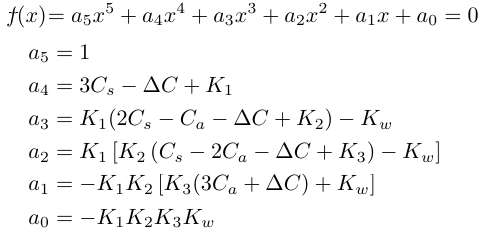|
<何にこだわったのか?>
既に2020年2月にこのテーマで話をしましたが、今回は次の点を工夫しました。
- いずれMathematicaで扱うことを考慮して方程式の複雑さ(次数)を気にしない。
- 正塩と酸の混合溶液も正塩溶液のみも酸のみも同じ方程式で解けるようにする。個別に扱うことはしない。
- 余剰H+(例えばHClの生成)の濃度ΔCを取り入れる。そうすれば緩衝作用が実感できる。
|
<モデル>
前回のモデルと同じ所は
- H3X の3段階解離モデルを採用する。K1, K2, K3 を用いる。
- X の保存則を用いる。
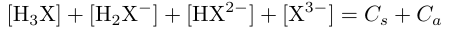
ここでCaはクエン酸濃度、Csは正塩濃度です。
違う所は
- H+の保存則にH2O から生じたOH-も取り入れる。H2O の解離定数 Kw が入る。
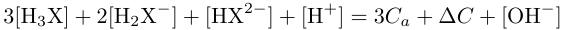
|
|
<プロトン濃度方程式>
x=[H+], y=[H3X]とすると次式(5次方程式)が得られます。
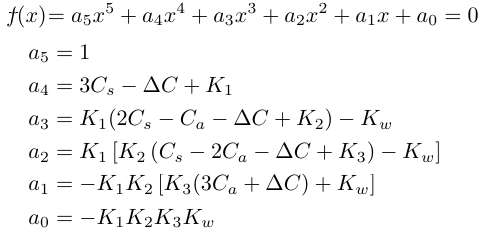
但し、Ca=0 かつ Cs=0 という溶液は(当然のことながら)除外します。
| <プロトン濃度方程式の数値解>
前回、近似解の改良という発想で4次方程式を解きましたが、今回は f(x)の符号が変わる区間をまず求め、そこで Newton-Raphson 法を適用することにしました。言語は Modula-2 です。
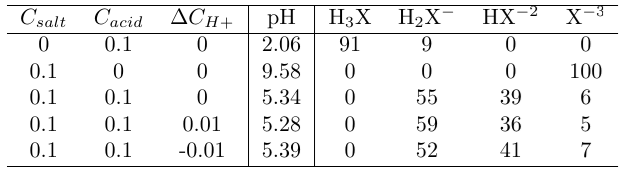
<適用例>濃度Cは mol/L 単位、組成はパーセント。
|