|
<原子の空間位置を計算する> CrystalPlane ではまず単位格子の中の原子位置をabc座標系で指定します。fccならabcはxyzと同じですが、hccはab間が120°でかつcの値を指定する必要があります。 次にxyz座標系で平行移動して、箱の中にN3個の原子を置きます。 Nは10〜20個とします。 |
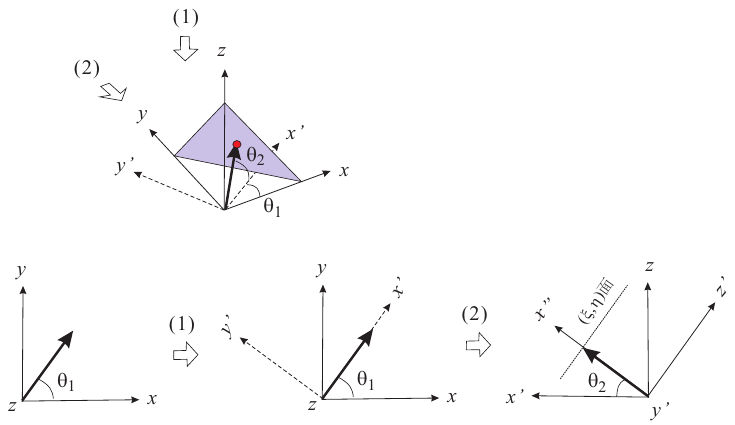
<座標軸を回転する> 下の図の陰影をつけたところが調べたい面だとします。そして面への垂線(x軸からの回転角度Θ1とxy平面となす角Θ2)が既に分かっているものとします。 まずz軸の周りにΘ1回転し、次にy軸の周りに-Θ2回転します。こうして得られた座標のうちでx=Dとなるものを拾い出せば当該面上の原子の配置が見えます。 通常はD=0としますが、異なるDでも拾えれば面上での結晶成長が見られます。 |
| |
|
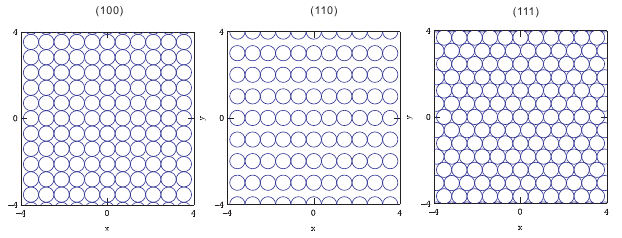
<面心立方格子ccpの表面構造>
| |
|
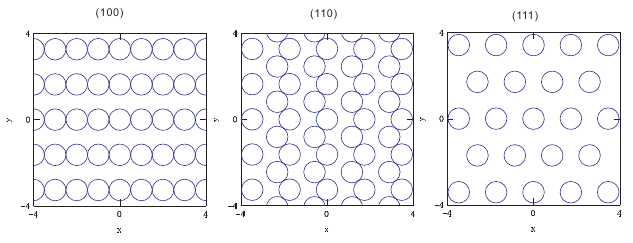
<六方格子hcpの表面構造>
| |
|
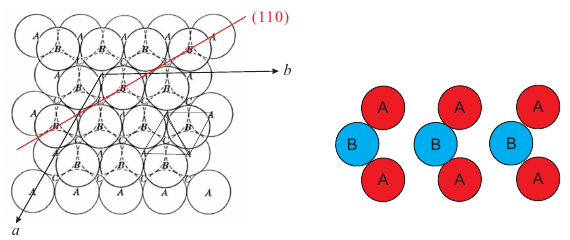
<hcp (110)の表面構造> プログラムのチェックの意味で図の(110)が正しいかを検証しよう。Part (1) ではビー玉で実現したが、右の図からも納得できる。 |
<hcp (110)面>
|
|
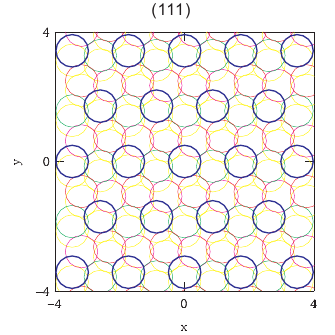
<hcp (111)の表面構造> (111)面に露出している原子はお互いに接触していませんが、奥行き方向の並びを見ると、原点から 85%, 71%, 56%, 42%, 21%, 12% の距離にみつかります。 |
<hcp の奥行き>
|