| <Python (Object Oriented Programming)>
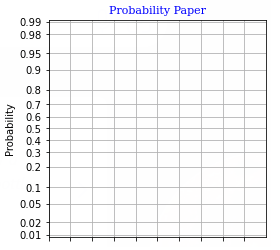
[Main] code2.2ccc_grid.py
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
#import numpy.random as rnd
import hwblines2 as hl
#import statpos as sp
eps = 0.01
xmin = 0.
xmax = 10.
xstep = 1.
ax = plt.axes()
ax.set_xlim(xmin, xmax)
ax.set_ylim(0.0, 1.0)
ax.set_aspect(xmax-xmin)
xtic = np.arange(xmin, xmax, xstep)
xlabels = np.array(['', '', '', '', '', '', '', '', '', ''])
ax.set_xticks(xtic)
ax.set_xticklabels(xlabels)
ax.set_xlabel('')
yax = hl.tic_label(eps)
ax.set_yticks(yax.tics)
ax.set_yticklabels(yax.labels)
ax.set_ylabel('Probability')
ax.grid(True)
font1 = {'family':'serif','color':'blue','size':11}
#font2 = {'family':'serif','color':'darkred','size':12}
plt.title("Probability Paper", fontdict = font1)
plt.show()
[Module] hwblines.py
import numpy as np
import hwbfiles as hf
from scipy.special import erfinv
class tic_label:
def __init__(self, eps):
feps = erfinv(1.0 - 2.0*eps)
def finvcumulat(y):
z = (1.0 - 2.0*eps)*erfinv(1.0 - 2.0*y)/feps
return 0.5*(1.0 - z)
p = np.array([eps, 0.02, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5,\
0.6, 0.7, 0.8, 0.9, 0.95, 0.98, 1.0-eps])
s = str(eps)
ss = str(1.0 - eps)
q = np.array([s,'0.02','0.05','0.1','0.2','0.3','0.4',\
'0.5','0.6','0.7','0.8','0.9','0.95','0.98',ss])
nticks = 15
r = np.arange(0.0, float(nticks), 1.0)
for i in range(nticks):
# print(p[i])
r[i] = finvcumulat(p[i])
self.tics = r
self.labels = q
self.nticks = nticks
self.finvcumulat = finvcumulat
def info(self):
print("Information on class 'tic_label'")
print('nticks:',self.nticks)
print('labels:',self.labels)
print('tick position:')
for i in range(self.nticks):
print(f"{self.tics[i]:,.3f}",end=" ")
print()
|
<Modula-2 (Structured Programming)>
[MAIN] MODULE cumulatPlot.MOD
FROM cumulative IMPORT gridPlot,・・・
FROM HgrWindows IMPORT openTextWin,initXDSgraph,・・・
FROM IO IMPORT WrStr, WrLn, ・・・
・・・
BEGIN
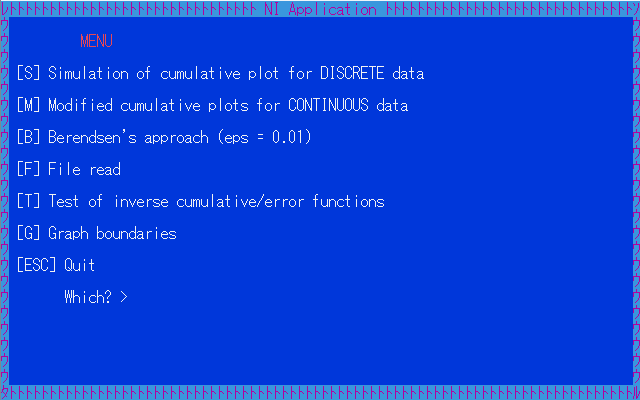
openTextWin(W1,'Graphic Application');
initXDSgraph(_big);
ticscale:= _Berendsen;
setBerendsenCoeff(0.01);
cXmn:= -1.5; cXst:= 0.0; cXmx:= 10.0; cXsp:= 1.0;
ticX.barleft:= cXmn;
setTicPos(ticscale);
scalePos();
whereXtic(ticX);
gridPlot(ticcumn,ticpos,Ntic,avrev, 0);
WrLn;
WrStr(' Want to generate a plotter file? (y/n)>');
IF CAP(WinAuxIO.GetKey())='Y' THEN
gridPlot(ticcumn,ticpos,Ntic,avrev, 2);
END;
・・・
変数定義とインポート宣言をかなり省略しました。テキスト・ウィンドウでテキスト形式のメニューを表示します(下図)。
[MODULE] cumulative
DEFINITION MODULE cumulative;
PROCEDURE gridPlot(VAR ticcumn: ARRAY OF LONGREAL;
VAR ticpos: ARRAY OF LONGREAL;
Ntic: INTEGER;
scalePos: LONGREAL;
dev: INTEGER);
・・・・・・
IMPLEMENTATION MODULE cumulative;
FROM SpecFunc IMPORT invErf,・・・
FROM HgrGlobal IMPORT graphsize,・・・
FROM HgrProtoType IMPORT LinLinFrame,・・・
FROM HgrLine IMPORT polyline,・・・
IMPORT HgrLow;
IMPORT HgrStrings;
IMPORT WinAuxLib, WinAuxIO, WinAuxStr;
FROM WinAuxIO IMPORT GetKey, CheckLngRealValue, hitKey;
FROM IO IMPORT WrStr, WrInt, WrLn, WrLngReal;
IMPORT Str;
PROCEDURE funBerendsen(y: LONGREAL): LONGREAL;
VAR
zy: LONGREAL;
BEGIN
IF y<=0.0 THEN
WrStr(' set to 0 to avoid overflow'); WrLn; zy:= 0.0;
ELSIF y>=1.0 THEN
WrStr(' set to 1 to avoid overflow'); WrLn; zy:= 1.0;
ELSE
zy:= cA_Berendsen * invErf(2.0*y - 1.0) + 0.5;
END;
RETURN zy;
END funBerendsen;
PROCEDURE gridPlot(VAR ticcumn: ARRAY OF LONGREAL;
VAR ticpos: ARRAY OF LONGREAL;
Ntic: INTEGER;
scalePos: LONGREAL;
dev: INTEGER);
CONST
TitleSize=4; Size=4; black=15; green=2; c1=13; c2=12;
Xlabl = "4.0"; Ylabl = "4.0";
Ymn = 0.0; Ymx = 100.0;
Xstep= 1.0; Ystep= 50.0;
eps = 1.0E-8;
VAR
i, ii : INTEGER;
ix, iy : INTEGER;
col1,col2: INTEGER;
xtit,ytit: ARRAY [0..31] OF CHAR;
u, v : ARRAY[0..1] OF REAL;
OK : BOOLEAN;
str : ARRAY [0..15] OF CHAR;
BEGIN
isRectangle:= isRect;
IF dev=0 THEN col1:= c1; col2:= c2; ELSE col1:=1; col2:= 1; END;
Str.Copy(xtit, 0C);
Str.Copy(ytit,'Probability (%)');
Str.Copy(LabelLrLtX, Xlabl);
Str.Copy(LabelLrLtY, Ylabl);
FOR i:=0 TO Ntic-1 DO
ticpos[i]:= funBerendsen(ticcumn[i]);
out("tic y-posn", i, ticpos[i]);
END;
iniplt(dev, 1.0);
TicPosition(FALSE); (* ticks out of frame *)
LinLinFrame(cXmn, cXst, cXmx, cXsp, cYmn, cYmn, cYmx, cYsp,
0, 0, 0, 0, Size, xtit, ytit, FALSE, 1.0);
FOR i:=0 TO Ntic-1 DO
IF (i=0) THEN
u[0]:= ticX.barleft;
u[1]:= ticX.barright;
v[0]:= 100.0*FLOAT(ticpos[i]); v[1]:= v[0];
polyline(u, v, 2, col3, 0, Size, 0, 0);
u[0]:= cXst; u[1]:= cXmx;
polyline(u, v, 2, col3, 0, Size, 0, 0);
ELSIF (i=Ntic-1) THEN
u[0]:= ticX.barleft;
u[1]:= ticX.barright;
v[0]:= 100.0*FLOAT(ticpos[i]); v[1]:= v[0];
polyline(u, v, 2, col3, 0, Size, 0, 0);
u[0]:= cXst; u[1]:= cXmx;
polyline(u, v, 2, col3, 0, Size, 0, 0);
ELSE
u[0]:= ticX.barleft;
u[1]:= ticX.barright;
v[0]:= 100.0*FLOAT(ticpos[i]); v[1]:= v[0];
polyline(u, v, 2, col3, 0, Size, 0, 0);
u[0]:= cXst; u[1]:= cXmx;
polyline(u, v, 2, col3, 0, Size, 0, 2);
END;
ix:= HgrLow.iscrx(ticX.label + ushift);
iy:= HgrLow.iscry(v[0] + vshift);
Str.Append(str,'%');
HgrStrings.justifystring(ix,iy, str, 0, chsize, base,base);
END;
u[0]:= cXst; u[1]:= u[0]; v[0]:= cYmn; v[1]:= cYmx;
LOOP
polyline(u, v, 2, col3, 0, Size, 0, 2);
u[0]:= u[0] + cXsp;
IF u[0]>= cXmx THEN EXIT END;
u[1]:= u[0];
END;
IF dev=2 THEN endplt END;
END gridPlot; ・・・・・・
|