|
<電圧と電流を同時に測る>
右図の装置(というほどのものではありませんが)を組みました。映ってはいませんが電源は 5V DC、バリオームは5kΩです。 これを用いて二種類の実験を行います。
|

|
|
<食塩水の I-V 関係>
0.001 mol/L の食塩水を試料とし、上図の装置でVとIの定常値を測ったところ右図の結果が得られました(d=40 mm)。 直線ではないのでオームOhm の法則は成り立っていません。 5V における接線の傾きは 1/ρ、ρ=980Ω、1.5Vではρ=4kΩです。ρは接合型トランジスタの微分抵抗とよく似ています。 抵抗R=V/I を算出すると、V=1.5ではI=0.06 mAなのでR=25kΩです。この値はテスターで測った前頁の値とオーダーが合います。 一方、V=5ではR=2.2kΩです。この値は独立移動の法則による抵抗値とオーダーが合います。 (注)このようなデータが得られたら、片対数グラフにしていわゆる Tafel プロットとするのが普通です。 |
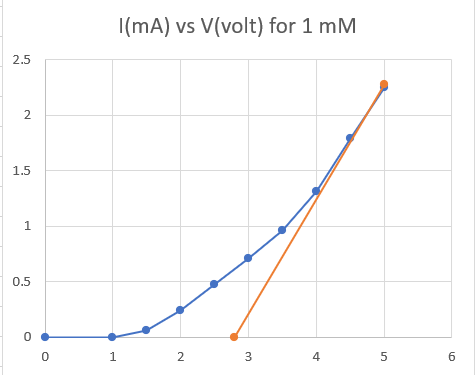
|
|
<食塩水の I-d 関係>
0.001 mol/L の食塩水を試料とし、d の値を変えながら電流を測って右図の青い曲線が得られました。電圧は左が5V、右が3Vです。 一方、赤い曲線は次式による計算結果です。 |
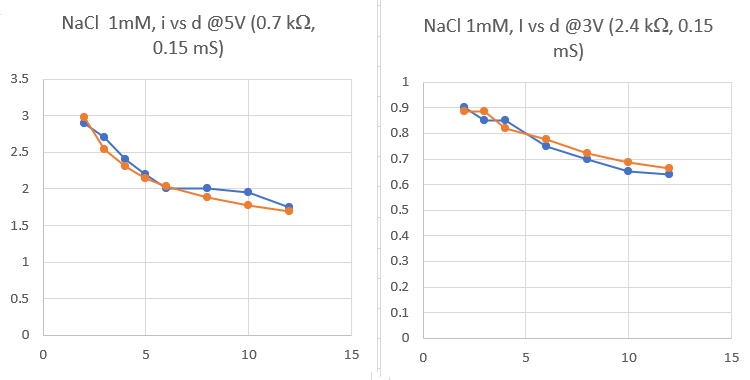
横軸は d/cm、縦軸は I(mA)。タイトルの括弧の中の数値は計算で用いたρとσ。 |
|
<ここまでのまとめ>
この式によってこれまでの実験結果が整理できます。まずR=Rbulk+ρ そのものはテスターで調べられること、Rbulkの値はVに依存しないこと、ρはVが高くなるほど小さくなることに留意します。
|
<オームの法則は絶対に成り立たないのか?>
オームの法則を成り立たせなくする元凶は ρ、つまり電極界面における電子移動の起きにくさでした。従って ρ を含まない実験をすれば オームの法則が成り立ちます。 「電解質溶液の伝導度測定」の専門家は、 電極の前面に電極を追加する、1kHz程度の交流で測定するなどの工夫をしてRbulkを正確に測っています( 例えば、高橋・天田、電気化学 29(1961)722)。 そうなるともはや素人の手には負えません(笑)。 <Chemical Impedance Spectroscopy, CIS> 交流の周波数を掃引してインピーダンス Z を測りましょう。このとき電気二重層の静電容量 Cdl をρ と平行に入れます。 そうすれば Z の実部に対して虚部をプロットした図は円弧になります。 これを発展させたのがCISです。 |