|
<食塩水が電気を通さない?>
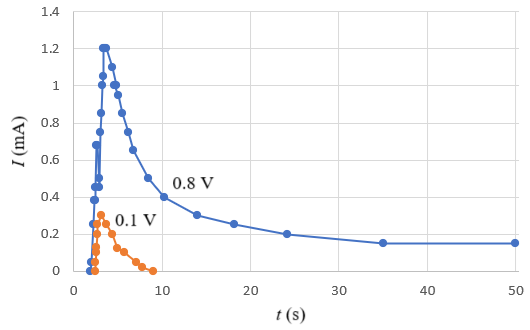
Part 2 で電極を0.001 mol/Lの食塩水に浸して定常電流を調べたところ 0.1 V(以下)で定常電流がゼロでした。つまり食塩水が絶縁体に変身しました。これは小中学校以来の常識に反します。 そこで電流の過渡変化という視点で調べ直ししました。ただし濃度を 0.01 mol/L と10倍にして電気を通しやすくしました。 右図がその結果です。V=0.8 では定常電流が流れています。この値は I=Vsteady/(Rbulk+ρ) であるとみなせます。Vsteady<V です。一方、V=0.1 では定常電流が流れません。この理由は、単に抵抗が大きくなったのではなく、電気二重層の形成によってVsteady=0 になったとするほうがいいと考えます。 |
<電流の過渡変化>
|
|
<Gouy-Chapman の電気二重層モデル>
電解質溶液に電場をかければイオンが電極に向かって移動して電流が流れます。これはイオンと電極との間で電子移動が起きなくても観測できます。もし電子移動が起きなければイオンは電極近傍に溜ま って電気二重層を形成し、電極の電場を遮蔽するので電流が流れなくなります。これが 0.1 V で起きていると考えられます。 この時イオンがBoltzmann分布に従うと考えて問題を数学的に解いたのが Gouy と Chapman です。Debye と Hueckelの有名な理論の10年前に発表されました。 |
<Gouy-Chapman の式>
静電ポテンシャルφと電気二重層の静電容量Cは次の通りです。 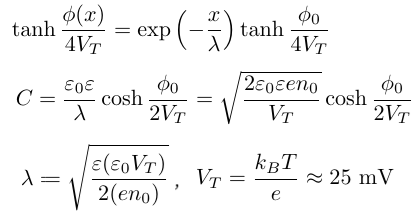
|
|
<過渡電流の起源>
V=0.1 の場合、電極に電圧をかけた瞬間から何が起きているかを考えてみます。
|
<定常電流が流れる場合>
V=0.8 ではイオンと電極の間で定常的な電子移動が起きますが、速度が不十分なためにイオンが溜って表面電荷を部分的に打ち消します。 後者によって減衰波形が現れたと考えます。ただしCの値は大きすぎて使い物になりません。Gouy-Chapman理論は電圧が高くなると電極面上の電荷分布を過大に評価しがちであると言われています。 |
|
<特性距離λ>
上で現れたλは方程式を無次元化するために導入したものです。濃度の平方根に反比例し、大きさはナノメートルのオーダーです。 平行平板コンデンサーの単位面積あたりの静電容量の式 C=ε0ε/d からの類推によってλは電極間隔と同等であるとみなせます。それを実用化したのがスーパーキャパシターと呼ばれるデバイス群です。従来の回路素子に比べて容量が何万倍にもなってエネルギー分野で新しいマーケットが生まれました。 |
<Debye距離 (Debye半径)>
λと同様にナノメートルのオーダーの数値ですが、電解質溶液の特性を表わす量としてDebye距離があります。有名なデバイ・ヒュッケルの理論の中で次のように定義されました。Iはイオン強度です。 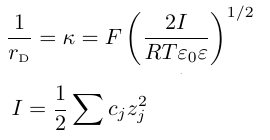
|