|
<問題>
Morse ポテンシャル V (右図)に対する シュレーディンガーの波動方程式 この解は原点で u(r)→rl、古典的転回点の外では指数関数的に減衰することが分かっていますが数値計算には直接的影響はありません。 |
<Morse関数>
この関数は平衡結合間距離r0で最小値、r→∞で一定値(解離状態に対応)を取ります。具体的な式は別のところに出ています。なお、ポテンシャル深さ D=100、r0=1(いずれも無次元量)。 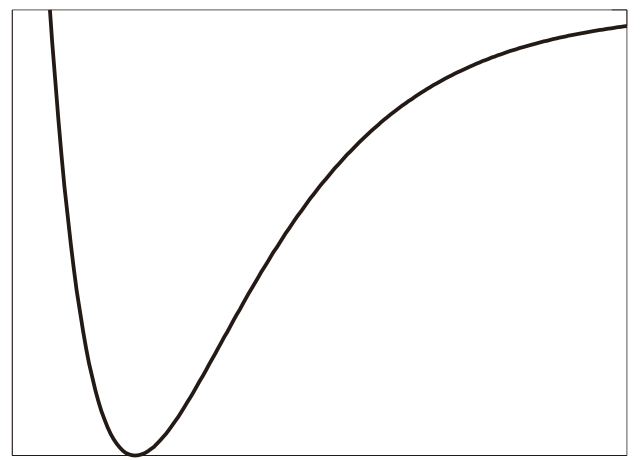
|
|
<固有値の計算法>
上に述べた振る舞いは Ev が固有値のときに成り立ちますが、そうでなければ u(r) は発散します。そこでまず E の初期値を決めたあと次のサイクルを踏みます。なおΔE=0.1 です。
|
<Wronskianの軌跡>
W=0 を横切るときのE値が Evです(v=0,・・・,8)。横切ったら直ちに次の固有値の探索に移ります。 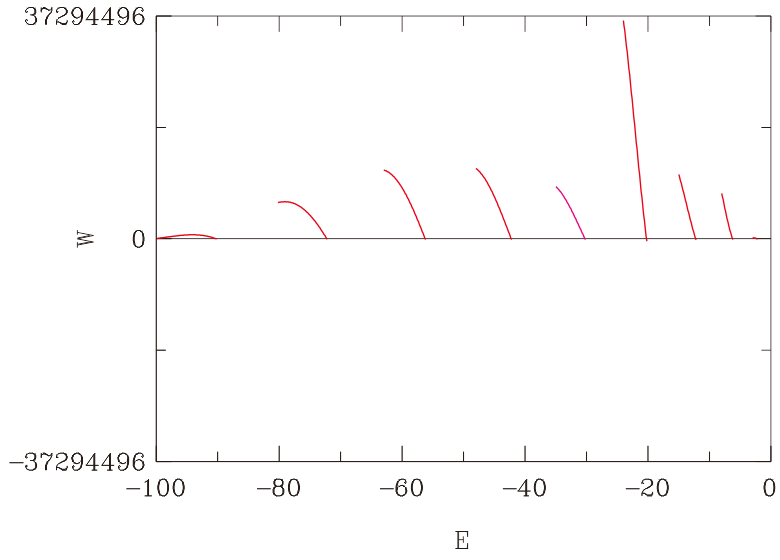
|
|
<固有値と固有関数:調和ポテンシャルによる試験>
厳密解が分かっている調和ポテンシャルに適用してプログラムにエラーがないことを確認しました。 
|
<固有値と固有関数:Morse ポテンシャル>
本番の答えです。横線は E0, E1,・・・, E8、赤い曲線は固有関数です。 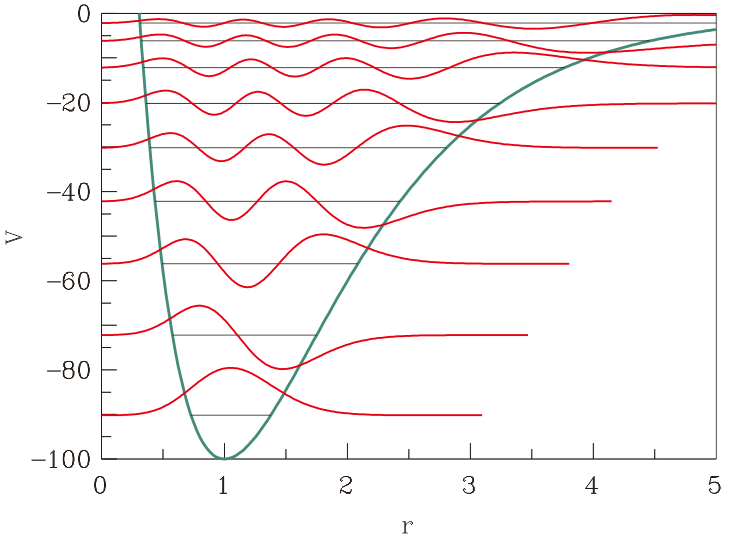
|