|
<分子をバネに見立てる>
分子ABがバネだとします。力で押しつければ縮みます。このとき、バネはポテンシャルエネルギーを持ちます。力学的仕事ができるという意味です。 いくら押しつけても壊れることはないので、押しつけた極限でのポテンシャルエネルギーは∞と考えてもいいでしょう。 力で引っ張ってもバネはやはりポテンシャルエネルギーを得ます。この時バネはどこまでも伸びることができ、やがて原子AとBはフリーになります。現実のバネが破断という不連続変化をするのとは違います。 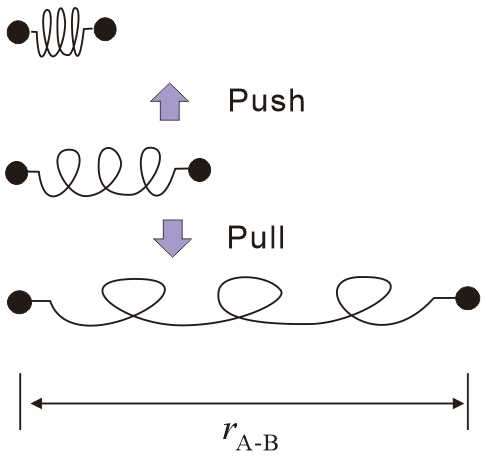
|
<Morseによるポテンシャルエネルギー曲線>
バネの伸び縮みの大きさとポテンシャルエネルギーの関係を表わした図がポテンシャルエネルギー曲線です。分子の世界ではP.M. Morse (1929) が発見した次の関数が有名です。なお -D 項を入れないこともあります。 この関数の形状は次の通りです。 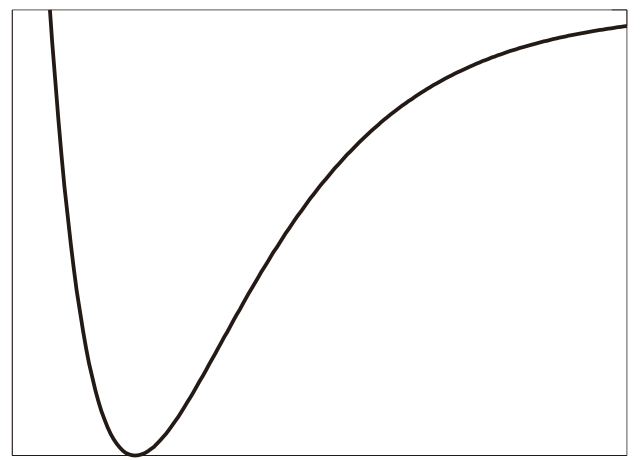
|
|
<自由振動するバネ>
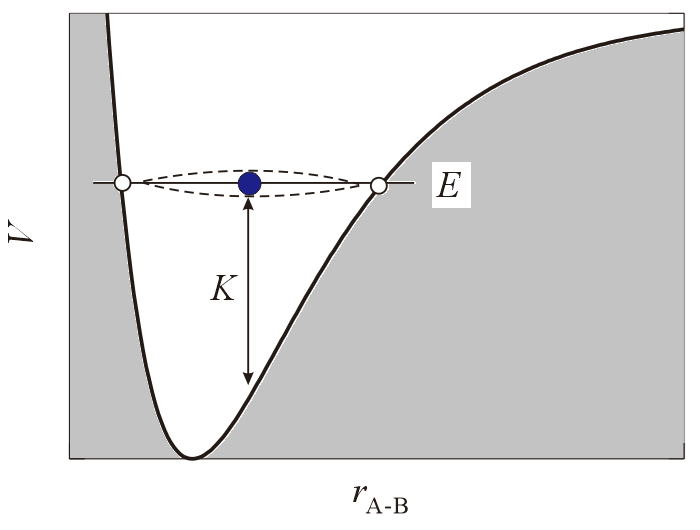
気体中の分子に近い状況は、巨大な宇宙船の中を浮遊するバネでしょう。バネは運動エネルギーKとポテンシャルエネルギーVの和 E を保持しながら振動し続けます。そのうちの1個のようすが下図に示されています。縦の矢印は K の大きで、速度の二乗に比例します。両端の○は古典的転回点 classical turning point です。この位置で向きを変え、速度はゼロになります。日常の世界では E が取る値に制約はありません。
|
<自由振動する分子>
分子の世界は量子力学が支配しています。そして分子振動はシュレーディンガーの波動方程式 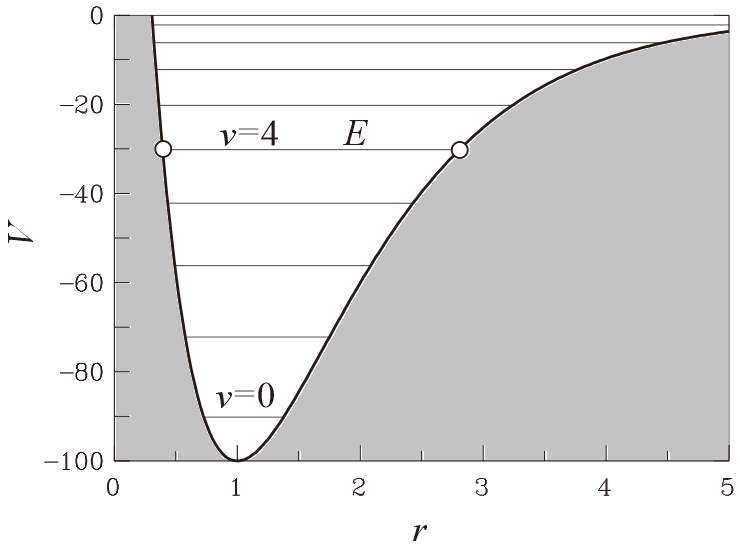
|
|
<Wolfram code (chemistry_morse.nb)>
次のコードは二種類の Morse ポテンシャル関数 fVmorse[r,dD,a,r0] と funMorse[x,dD,a] を定義し、funMorse のグラフを D=1~100, a=0.5~5 で描きます。 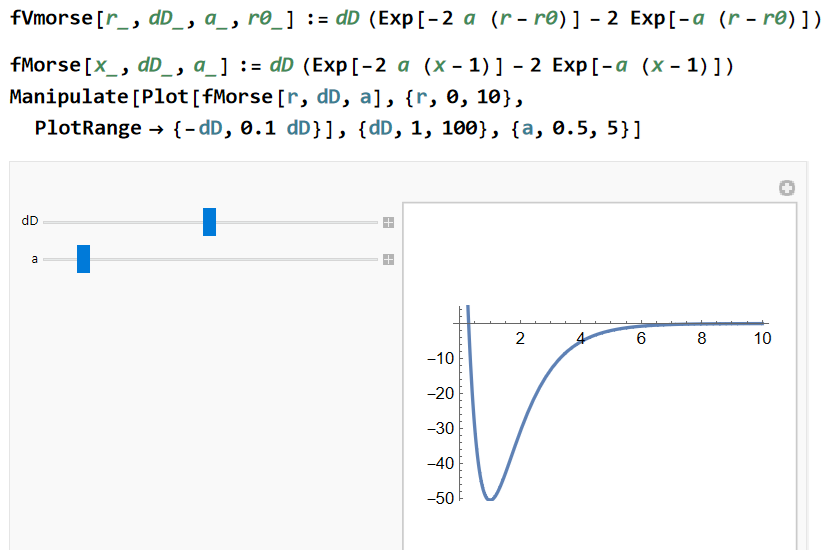
次のコードでは E=-g dD に対する古典的転回点 rt を求めています。最初、首をかしげたくなるような結果が得られましたが Simplify の適用で納得のいく式となりました。 
次のコードはこれらの古典的転回点の間で原子が振動するようすをアニメーション化します。ただし、Morseポテンシャルで点を定義しますが、ダイナミックスは調和ポテンシャル(つまり単振動)の動きで近似しています。g が小さいと微小振動、大きいと大振幅振動です。後者では両端でもっとゆっくりと動くべきでしょう。 
|
|