|
<How to calculate K-matrix>
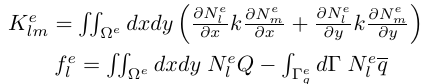
によって K-matrix を計算します。線形のshape functionでは偏微分すると定数でしたが、一般には計算が面倒です。 <Rectangular Elements 四角形> まず (2) の最初の図について計算します。scaled shape function は です。これを実際に偏微分し積分するとK11に比例する量として |
<K-matrix by Wolfram (1)> 左の計算をWolfram で実行したのが下です。 
N1 の式を書き入れるだけでよいこと、解が分数式で得られるところ(そして手計算で必須の検算が必要ないこと)はさすがです。 |
|
<Triangular Elements 三角形> (3) の図は正三角形でしたが、ここでは底辺と高さが任意の直角三角形を取り上げます。スケーリングによて 0<X,Y<1 に変換します。斜辺の真ん中のNodeに対しては N3=4XY という shape function が得られます。これを用いて次の計算をします。積分範囲Δは三角形なので、Xの積分とYの積分に分離できないので計算は面倒です。 |
<K-matrix by Wolfram (2)> 左の計算をWolfram で実行したのが下です。積分範囲に要注意です。 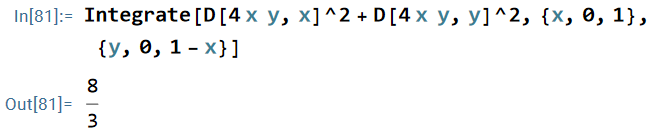
|