|
<Linear shape function N(x,y)>
線形モデルでは一般に N(x,y)=α+βx+γy で表わされ、Elementの原点で N=1, その他の頂点で N=0 です。 頂点の番号を反時計回りに i,j,k とします。もし j を原点とすれば k,i が「その他」です。 βiとγiは xj, xk, yj, yk で表わされます(O.C. Zienkiewicz and K. Morgan の Text p.127)。 この Text で扱う三角形 Element は底辺が横軸に平行なので、 頂点の座標は (0,0), (a,0), (a,b) で表わせます。直角三角形なら最後が (0,b) または (b,0) です。
|
<K-matrix> 2次元Finite Element Method(有限要素法)ではK-matrixが次の最初の式になります(FEM1.html)。 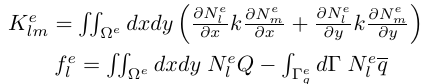
この式はコンパクトにKeφe=feと書けます(Text p.133)。φはNode における解の値です。 結局 Klm=(βlβm+γlγm)×(Element の面積) です(ただし面積は打ち消し会います)。 |
|
<方式1>

|
|
|
<方式2>
方式1では If が何度も出てきて鬱陶しいので cyclic という関数を作りました。cyclic[1] なら j=2, k=3 です。

|
|