|
<多様な固体表面>
固体が気体・溶液に接していれば分子が常に固体表面と衝突します。もし分子と固体表面との間に相互作用が働かなければ分子は何事もなかったように去って行くでしょうが、
実際にはなにがしかの相互作用、つまり引力が働くのが普通です。少しでも引力が働けば表面に滞在する時間がゼロでなくなります。
ちょうどよい引力では、表面構造を壊すことなく分子が表面に滞在します。一般にA+B-->C の反応に対する固体触媒では A, B のどちらか、あるいは両方が吸着して反応が進みます。 |
<吸着材料>
吸着材料をうんぬんする時は、吸着と脱離が繰り返せることを前提とします。その典型が、吸湿剤としてよく使われるシリカゲルです。電子レンジで加熱すれば水分が抜けます。 シリカゲルの表面には水分子がすっぽり収まるような洞穴があるのです。おそらく (SiO2)n とH2O の間で水素結合ができているのでしょう。 燃料電池用水素タンクとして可能性があるのが水素吸蔵合金です。この場合、吸着の枠組みを超えてH2が原子状になって結晶内部に侵入しますからスーパー吸着といってもいいでしょう。その際体積が膨張します。圧力を下げれば外部に水素取り出せます。 |
|
<吸着のモデル>
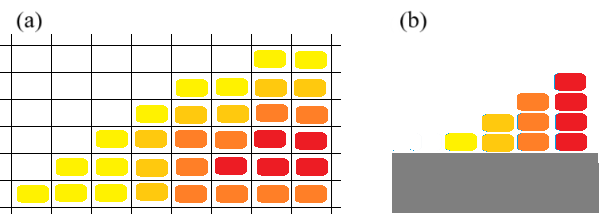
右図(a)のように分子が吸着できる場所(吸着サイト)が長方形状に配置されているものとします。色は吸着層の厚さに対応します。図(b)に示すように白は未吸着、黄色は単層、赤は4層です。以後、i 層からなるサイト数をNiとします。吸着と脱離に対応する速度式は次のように書けます。 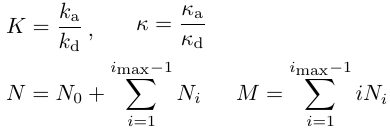
|
<吸着の模式図>
|
|
<Langmuirのモデル>
imax=2 であれば N=N0(1+Kp), M=N0Kp ですから |
<BETのモデル>
imax=∞ であれば無限級数を計算して 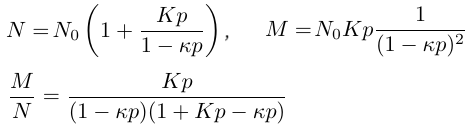
|
|
<Wolfram code (chemistry_adspn.nb)>
次のコードでは Langmuir モデルに基づいて吸着量 M/N=funLanfmr を横軸 pK に対してプロットします。K=10nで n が 可変です。 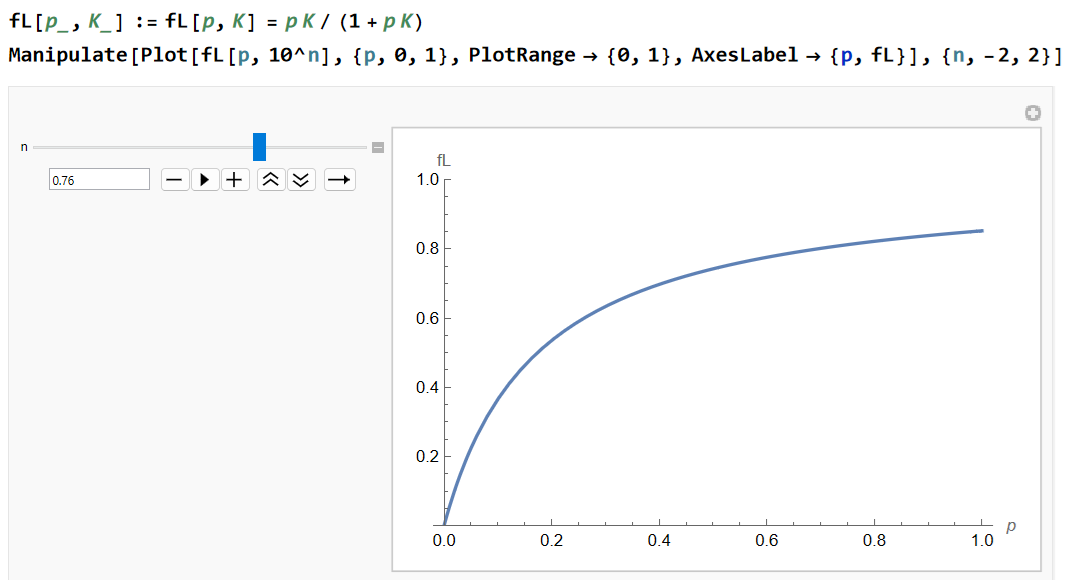
次のコードでは、BET モデルに基づいて吸着量 M/N=funBET を x=Kp に対してプロットしています。c=10nでnが可変、またグラフの縦軸範囲も可変です。なお、x=1 での発散を防止しています。 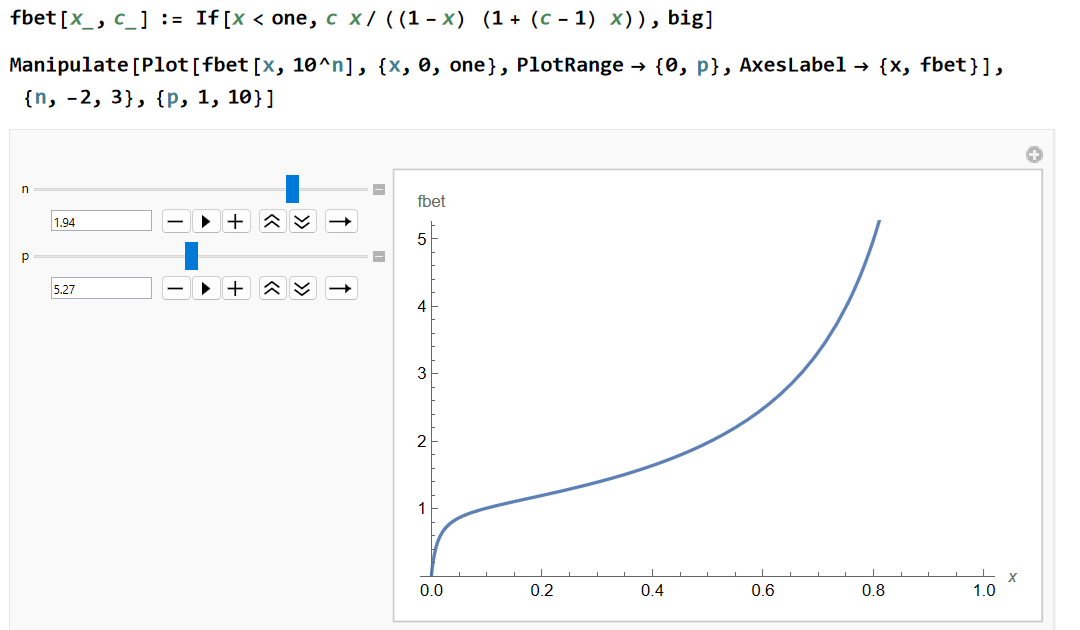
|
|