読んで字のごとく物質が拡がり散らばっていくことで、コーヒーに垂らした一滴のミルクの動きが例としてよく挙げられます。しかし、この系は意外と複雑で、多分液体ミルクの表面からエマルジョンが分離しブラウン運動をしながら拡散していくと考えられます。その際、コーヒーとの密度差やコーヒー内の対流でさらに複雑になります。コーヒーを使うのならむしろコーヒー層の上に水層を置くほうがいいでしょう。いずれにせよ媒質の中を分子または微粒子がランダム運動した結果拡がったという Langevin のモデルで理解できます。そして媒質との間の摩擦で拡散係数 が決まります。その他、濾紙やコンクリートにおける拡散は、微細な隙間に染みる過程であると理解できます。

Fuckの法則「物質のフラックス（流束）J は濃度 c の勾配に比例する」の比例係数が拡散係数 D です。それと物質の保存則「濃度の時間変化とフラックスは釣り合う」を組み合わせて拡散方程式が得られます。D は大抵 10^-9〜10^-11m²/s の範囲にあります。

以後解析的に表わされる過程を考えます。この問題の初期条件は原点 (0,0) に集中した一点です。 そのような解は

二種の液体が界面を介して接触しているものとします。一般に界面はぼやけますが、t=0 でクリアな界面になるものとします。 そのような初期条件に対応する解は

扱いやすい大きさの数値にするために長さを mm 単位で表現することにします。そうすると D=10^-3〜10^-5mm²/s となります。

次のコードは二次元拡散を t と range（縦軸の最大値）を可変として表示します。 P^B(x,y,t) を fB[x,y,t] で表わしています。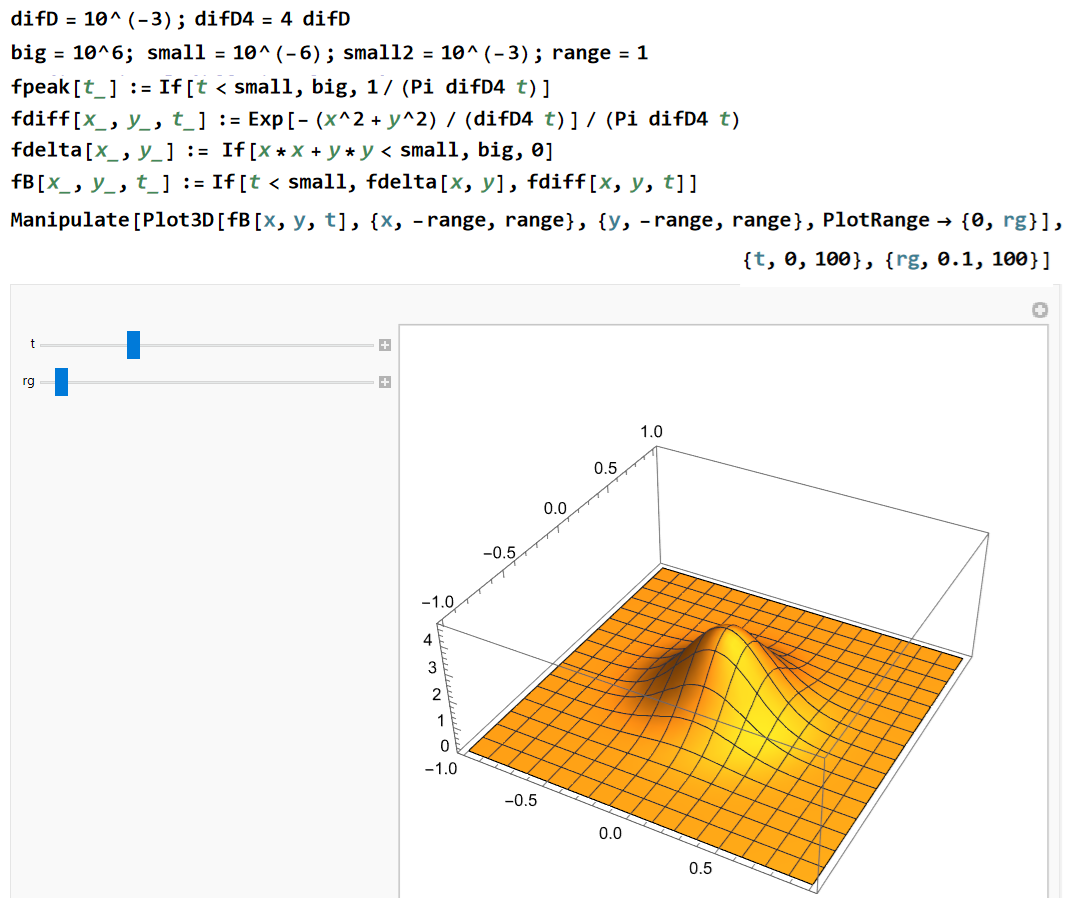

次のコードでは、界面を介して物質A,Bが相手の中に一次元で拡散する過程を 6個の時間について描いています。P^C(x,t) を fC[x,t] で表わしています。どちらかの拡散も同程度で進むとしています。その真逆な例が多孔質体に染み込む過程です。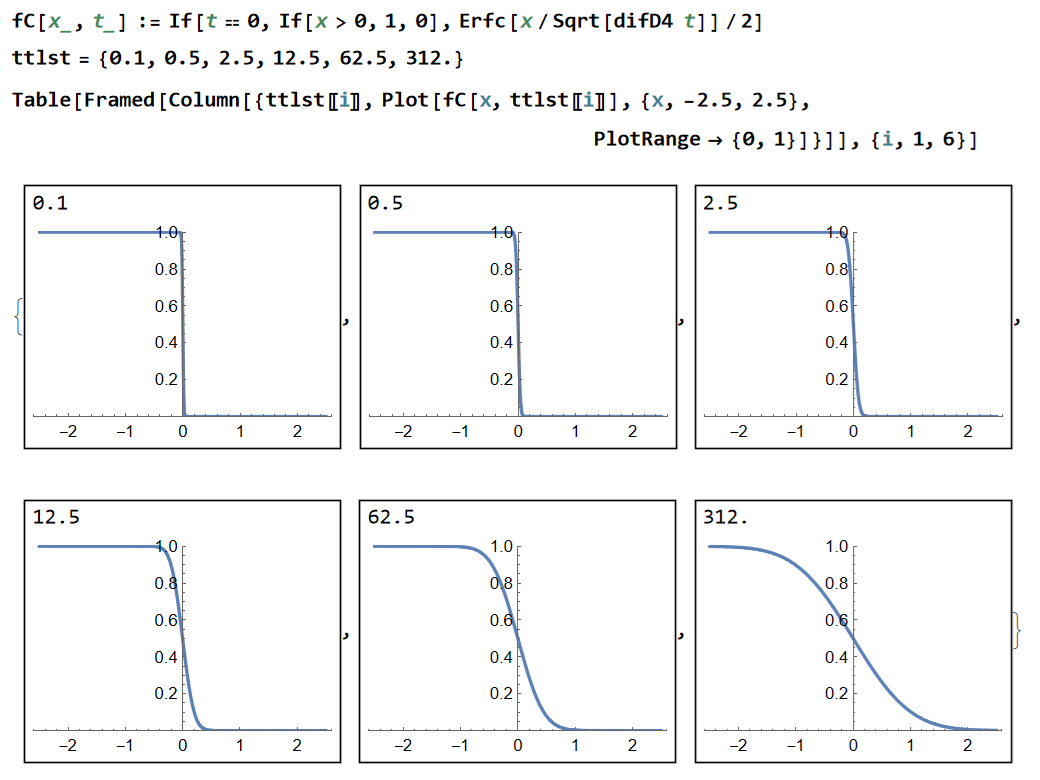