|
<理想気体>
pV=nRT の関係(Boyle-Charles の法則)が成り立つ気体のことを理想気体といいますが、実際の気体で調べてみると圧力を低くしないと成り立ちません。理想という言葉の意味合いは「こうありたい」というよりは「こういうのがあるとして話を進めてみよう」といったところです。低圧ということは、分子どうしが衝突する頻度が低いことを意味しますから、もし分子に大きさがなくて点であれば衝突そのものが起きませんから理想気体になると考えられます。 現実には成り立たないから不要かといえばそんなことはなくて、精度が気にならなければ問題ありません。また、理想気体の式を仮定することで多様な粒子系の理論が発展させられます。 |
<現実気体と van der Waals の関係式>
現実の気体分子には大きさがあり、弱いながらも引力を及ぼし合います。それらを考慮した式が次の van der Waals の状態方程式です。二つのパラメータ a, b の値ををうまく決めれば広い圧力範囲で実際とよく合います。
次の式に変形してグラフ化します。v=V/n=モルあたりの体積です。分子に大きさがあるので v>b とします。 |
|
<Wolfram code
(chemistry_vdw.nb)
> 次のコードで p(v)関係を表わす関数 fp2[v,T] を定義しました。a,b はCO2に対応するパラメータ、Rは気体定数です。T は仮の値、cLim は十分に大きな任意の値です。以後、単位は気にせずに話を進めます。 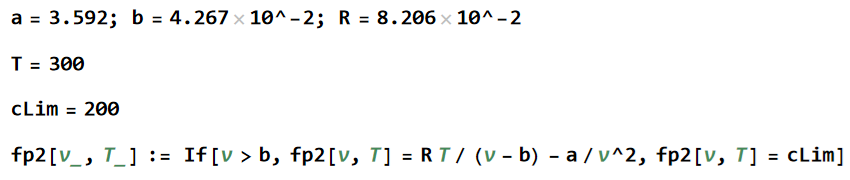
Wolfram の強みはアニメーションで発揮されます。下のグラフは体積 v に対する圧力 fp2 の関係を示しています。スライダー(上が 100≤ T≤500, 下が 0.5≤vx≤ 3)を移動させるだけで温度 Tと圧力の上限 vx が自由自在に変えられます。今のパラメータ値はT=259, vx=0.855 です。 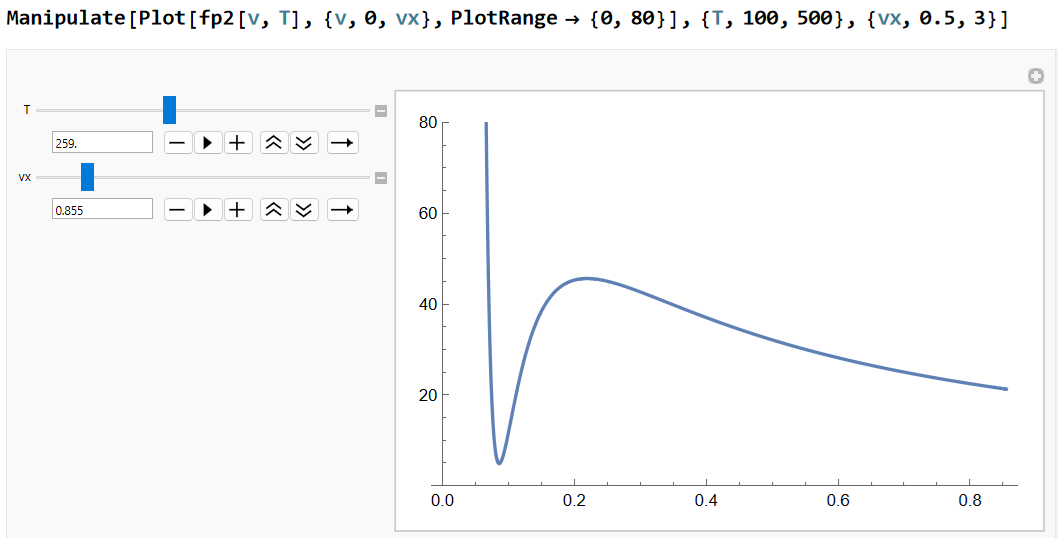
原点付近の凸凹はいかにも不自然な振る舞いです。そこで下図のオレンジのような修正が提案されました。水平線でもって等面積の領域に分離されています。オレンジに変えても力学的仕事の量 ∫pdv が変わらないので修正が正当化されます。なお計算法はかなり近似的です。 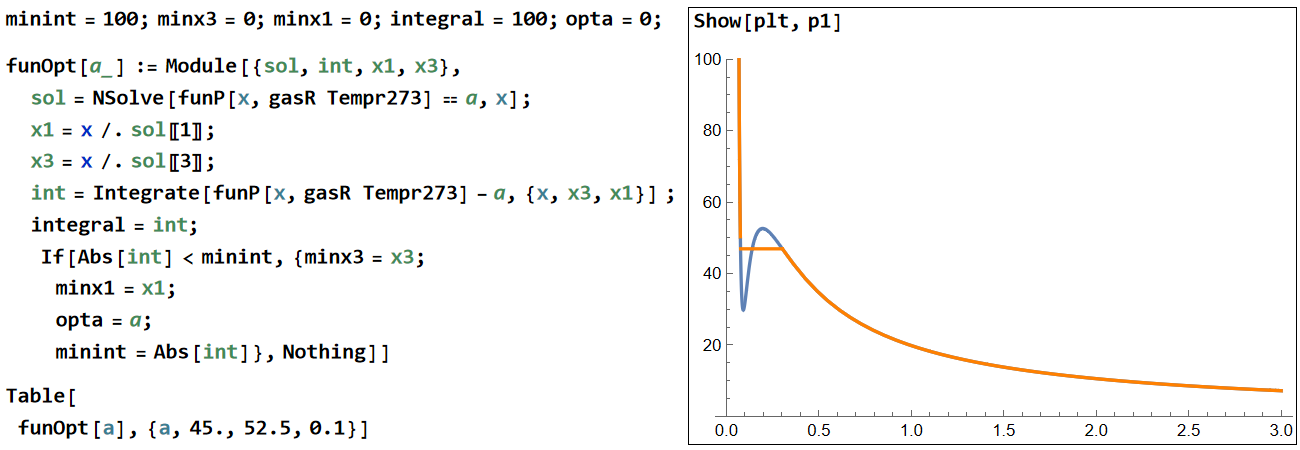
|
|