物質をミクロに見れば原子・分子が常に熱運動をしていることが分かります。その運動が絶対温度TでエネルギーEの状態にあれば存在確率が exp(-E/k_BT)に比例するというのがBoltzmannの法則で、k_BがBoltzmann定数です。 対象とする系が質量mの気体であれば E=(1/2)mv²ですから速度ベクトルvの成分(v_x,v_y,v_z)はそれぞれ

分子の速度は速度ベクトルvの大きvで定義するのが妥当でしょう。そのデカルト座標系の表現ですが球座標系 (v,θ,φ) で表し、v依存性を取り出すと

分布がある量の代表値に平均値とモード値（最頻値）があります。 まずvの平均値v_avは

温度が下がるのに速くなるという実験があります。 ノズルビームといって対象分子をH₂やHeに混ぜてノズルから吹き出します（強力な排気系が必要）。すると、軽くて速い分子に追い立てられて対象分子も速くなります。それと同時に断熱膨張をするために温度が下がります。 速度分布は近似的に次式で表わされます。Vはビームに沿った移動速度、Cは規格化定数です。

次のコードで分子速度 v の分布を表わす関数 funV[v,T,W] を定義しました。Tは絶対温度、Wは分子量です。Manipulate[Plot[･･･]]でT,W,横軸の上限 vrange を制御してグラフが描けます。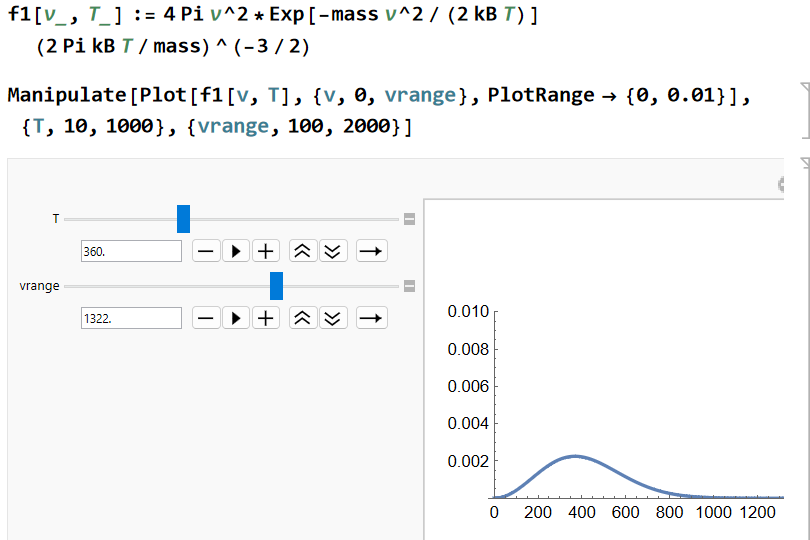

次のコードは、ノズルビーム中の N₂分子の速度分布ですが、実験条件によって形は大きく変わります。

次のコードで、いくつかの分子の分子量と平均速度の一覧表ができます。