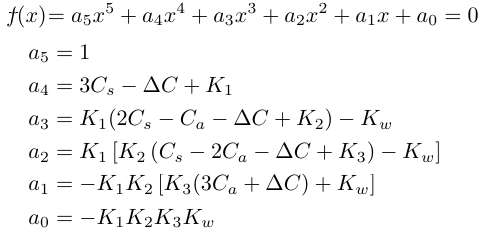酸性緩衝液の簡単な例は、酸 HX と塩 AX （A=Na, K, etc.）の混合溶液です。X^-を共通イオンといいます。AXは100%電離しますが、HXは一部しか電離しません。 もし何らかの理由でH⁺が増えても、かなりの部分がHXとなって排除されるのでpHの変化はわずかなものとなります。これが緩衝作用です。濃度と解離定数Kが分かれば緩衝液のpHは近似的に計算できます。

ここでは三塩基酸であるクエン酸H₃Xについてプロトン濃度[H⁺]を近似計算せずに求めます。まず平衡を表わす式は

X （1価〜3価の負イオン）の保存則は

次にH⁺の保存則は

x=[H⁺], y=[H₃X]とすると次式（5次方程式）が得られます。

• C_a=0 であれば根は正塩のプロトン濃度(<10^-7)になります。
• C_s=0 であれば酸単独になるのでプロトン濃度は 10^-7より大きくなります。
• もし逐次近似的に根を求めるのであれば初期値の選定に注意が必要になります。 参考2(2025)では f(x_i)とf(x_j)で符号が変わるような区間[x_i, x_j] を求めてからNewton-Raphson法を適用していますが、完璧ではありません。Mathematicaならどう処理するか見てみましょう。

(1) funcHwo という名前で f(x) を定義します。

(2) クエン酸塩が 0.2 mol/L, クエン酸が 0 mol/L のとき（つまり塩のみのとき） 5番目の解から pH=9.728 であることが分かります。ちなみに上記の近似計算でも pH=9.728 でした。

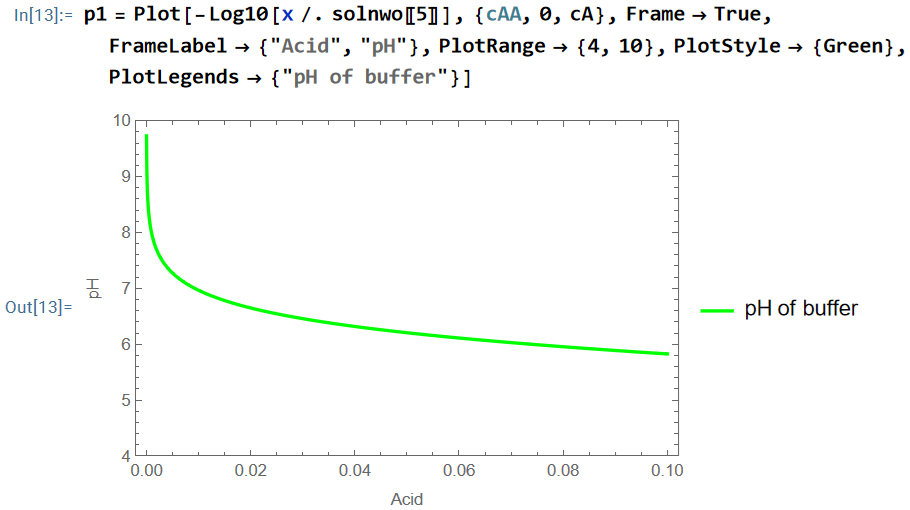
(3) クエン酸塩が 0.2 mol/Lで余剰[H⁺]が 0 の時, クエン酸を 0〜0.1 mol/L とすると pH がどう変わるかを示しています。

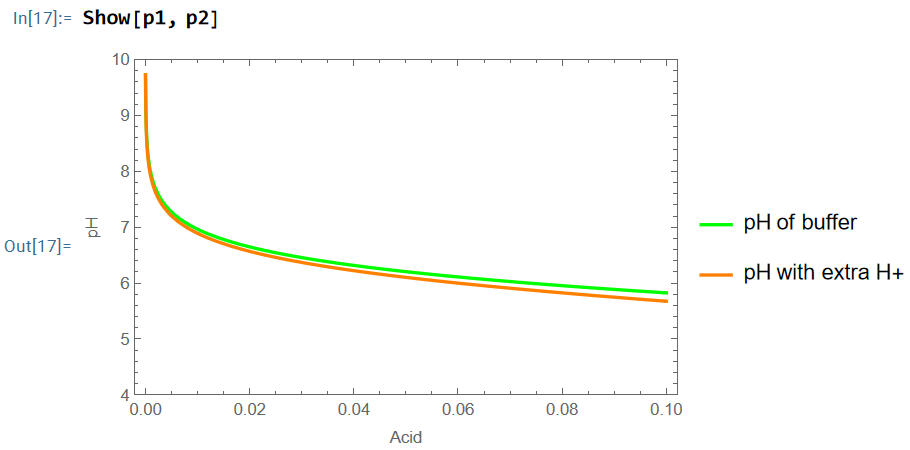
(4) この緩衝液にクエン酸の50%の H⁺（共通イオンを持たないHCl等）が加わればpHがどれだけ小さくなるかを示しています。pHが変わらなければ緩衝作用は完璧です。

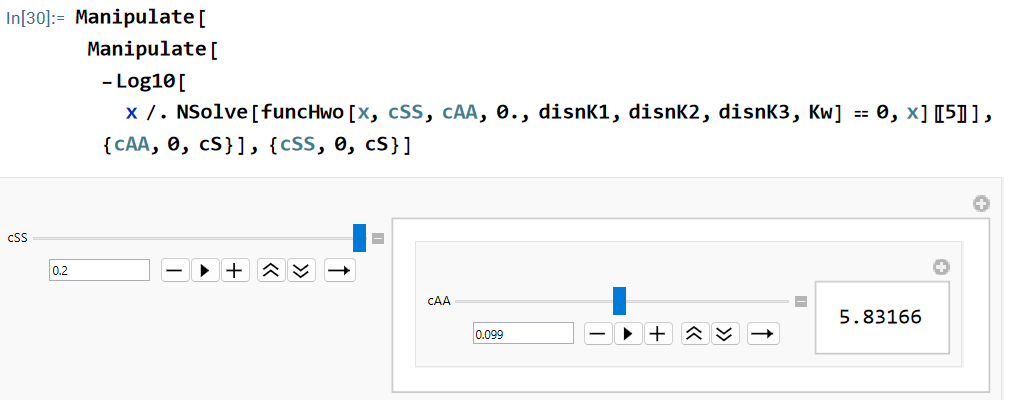
(5) クエン酸塩濃度 cSS とクエン酸濃度 cAA をスライダーで選択して pH を表示させます。