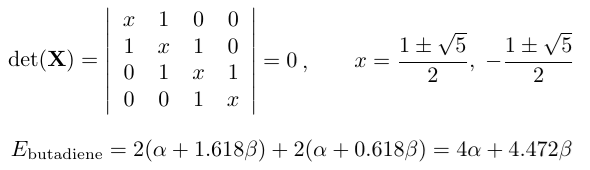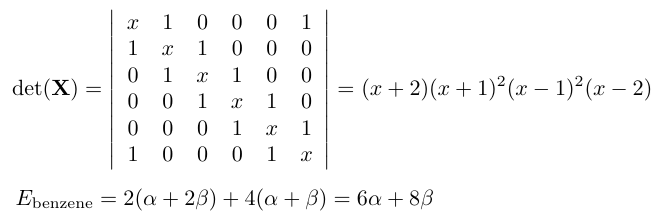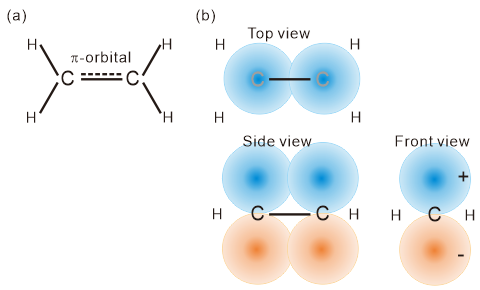
最も簡単なπ電子系はエチレンでしょう。右図(a)で直線はσ結合の化学結合、点線がπ結合を示します。両方合わせて二重結合ができます。図(b)はπ分子軌道(pi-MO)を様々な方向から眺めた図です。複素数なのであくまでも「感じ」です。このMOにはC-C軸上に節面がないので電子は二つのC原子の間を行き来して化学結合に寄与します(次のMOからは節面が現れます)。

もしMOが正確なら Hφ_j= Eφ_j というSchrödinger方程式を満足しますが実際には近似解 E_j=<φ_j|H|φ_j>/<φ_j|φ_j> しか得られません。そこでφ_jを原子軌道χ_iで展開してで最も良い近似値で満足することにします。こうしてx=(α-E)/β についての行列式が導かれます。ここでαはクーロン積分、βは共鳴積分(原子ij間に結合があれば取り入れる)と言います。

エチレンの場合、C₁とC₂にπ電子があるので右の行列式を解けば x=±1 です。x=-1にπ電子が2個入るので全エネルギーは右の通りです。

C₁〜C₄にπ電子があるので次の行列式と解が得られます。

エチレン2個分のエネルギーより 0.472β だけ低い(絶対値でいえば大きい) のはC₂とC₃の間にもπ結合ができているためです。このエネルギーを非局在化エネルギーといいます。

C₁〜C₆にπ電子があるので次の行列式と全エネルギーが得られます。

Kekulé構造(エチレン3個分)より 2β 低いことでいわゆる芳香族性が説明できます。

(1) エチレンのπ電子エネルギー。次のコードで 2x2 の行列を定義し、表示し、行列式を解き、電子2個のエネルギーを算出します。

(2) ブタジエンのπ電子エネルギー。次のコードで 4x4 の行列を定義し、行列式を解きます。

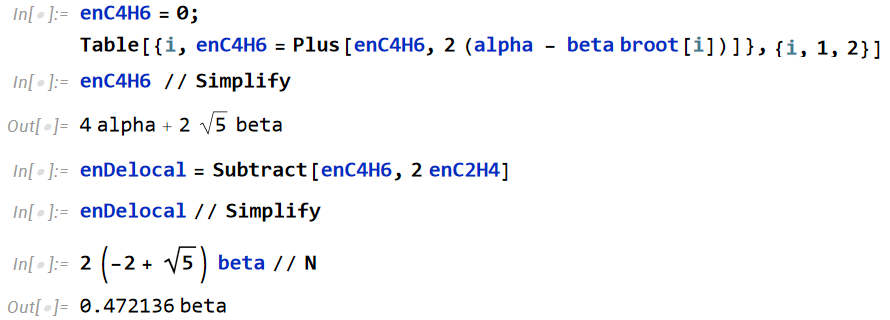
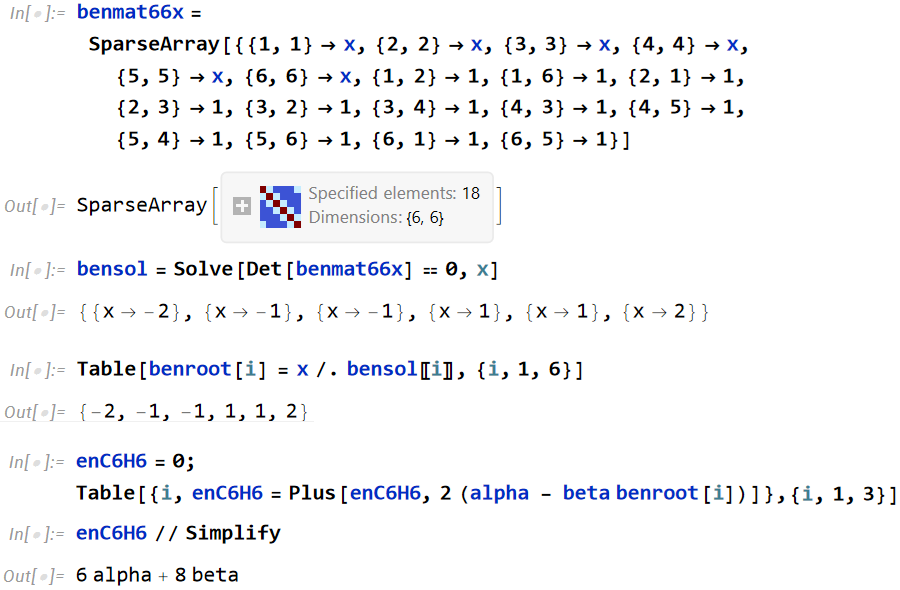
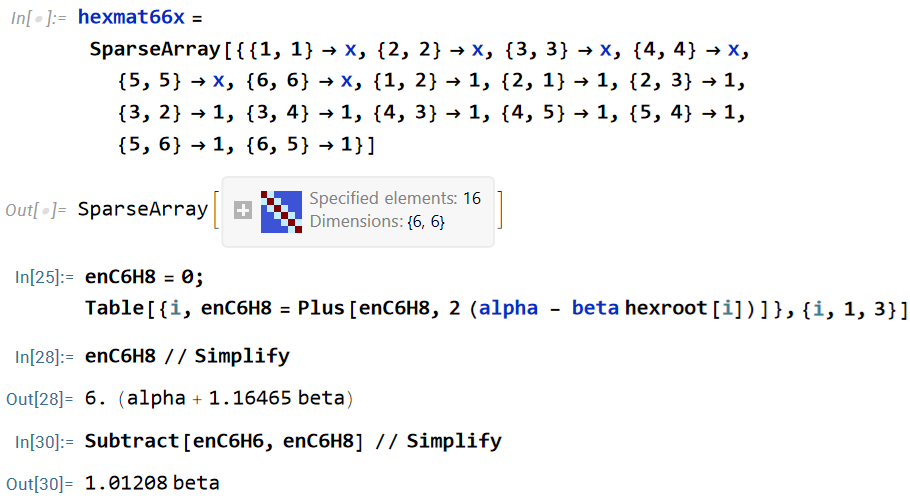
(3) ベンゼンのπ電子エネルギー。次のコードで 6x6 の行列を定義し、行列式を解き、π電子全部のエネルギーを出します。